题目内容
13.(1)求过直线x-2y+3=0和2x+y-4=0的交点,斜率为1 的直线方程;(2)过点A(-1,2)的直线l的倾斜角β是直线l1:2x-y+1=0的倾斜角α的2倍,求直线l的方程.
分析 (1)联立方程组得交点,利用点斜式,可得直线方程;
(2)利用二倍角公式求出直线的斜率,即可求直线l的方程.
解答 解:(1)联立方程组$\left\{\begin{array}{l}2x+y-4=0\\ x-2y+3=0\end{array}\right.$解得x=1,y=2 …(2分)
所以直线方程为y-2=1×(x-1),即为:x-y+1=0. …(5分)
(2)k1=tanα=2,$k=tanβ=tan2α=\frac{2tanα}{{1-{{tan}^2}α}}=\frac{4}{1-4}=-\frac{4}{3}$…(8分)
$y-2=-\frac{4}{3}(x+1)$,即:4x+3y-2=0…(10分)
点评 本题考查直线方程,考查学生的计算能力,属于中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
8.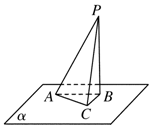 如图所示,三棱锥P-ABC的底面在平面α内,且AC⊥PC,平面PAC⊥平面PBC,点P,A,B是定点,则动点C的轨迹是( )
如图所示,三棱锥P-ABC的底面在平面α内,且AC⊥PC,平面PAC⊥平面PBC,点P,A,B是定点,则动点C的轨迹是( )
 如图所示,三棱锥P-ABC的底面在平面α内,且AC⊥PC,平面PAC⊥平面PBC,点P,A,B是定点,则动点C的轨迹是( )
如图所示,三棱锥P-ABC的底面在平面α内,且AC⊥PC,平面PAC⊥平面PBC,点P,A,B是定点,则动点C的轨迹是( )| A. | 一条线段 | B. | 一条直线 | ||
| C. | 一个圆 | D. | 一个圆,但要去掉两个点 |
3.($\sqrt{x}$-$\frac{2}{x}$+1)7的展开式中x3的系数为( )
| A. | -1 | B. | 1 | C. | -7 | D. | 7 |