题目内容
8.长方体ABCD-A1B1C1D1中,AB=$\sqrt{2}$,BC=AA1=1,则BD1与平面ABCD所成角的大小为30°.分析 连结BD、BD1,由D1D⊥平面ABCD,得∠DBD1是BD1与平面ABCD所成角,由此能求出BD1与平面ABCD所成角的大小.
解答  解:连结BD、BD1,
解:连结BD、BD1,
∵长方体ABCD-A1B1C1D1中,D1D⊥平面ABCD,垂足为D,
∴∠DBD1是BD1与平面ABCD所成角,
∵AB=$\sqrt{2}$,BC=AA1=1,
∴BD=$\sqrt{2+1}$=$\sqrt{3}$,BD1=$\sqrt{3+1}=2$,
∴sin∠DBD1=$\frac{D{D}_{1}}{B{D}_{1}}$=$\frac{1}{2}$,
∴∠DBD1=30°.
∴BD1与平面ABCD所成角的大小为30°.
故答案为:30°.
点评 本题考查线面角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
17.将函数y=sin(x+$\frac{π}{6}$)(x∈R)的图象上所有点的纵坐标不变横坐标缩小到原来的$\frac{1}{2}$,再把图象上各点向左平移$\frac{π}{4}$个单位长度,则所得的图象的解析式为( )
| A. | y=sin(2x+$\frac{5}{6}π$) | B. | y=sin($\frac{1}{2}$x+$\frac{1}{6}$π) | C. | y=sin(2x+$\frac{2}{3}$π) | D. | y=sin($\frac{1}{2}$x+$\frac{5}{12}$π) |
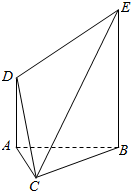 如图,△ABC为等边三角形,D,E是平面ABC同一侧的两点,DA⊥平面ABC,EB⊥平面ABC,EB=2DA.
如图,△ABC为等边三角形,D,E是平面ABC同一侧的两点,DA⊥平面ABC,EB⊥平面ABC,EB=2DA. 如图,已知在直四棱柱ABCD-A1B1C1D1中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.
如图,已知在直四棱柱ABCD-A1B1C1D1中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.