Question

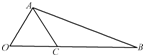如图，∠AOB=60°，OA=2，OB=5，在线段OB上任取一点C，试求：
（1）△AOC为钝角三角形的概率；
（2）△AOC为锐角三角形的概率．

Answer 1

考点：几何概型

专题：应用题,概率与统计

分析：（1）本题是一个等可能事件的概率，试验发生包含的事件对应的是长度为5的一条线段，满足条件的事件是组成钝角三角形，包括两种情况，第一种∠ACO为钝角，第二种∠OAC为钝角，根据等可能事件的概率得到结果；
（2）由已知条件利用勾股定理求出△AOC三个角都是锐角时1＜OC＜4，由此能求出其概率．

解答： 解：（1）由题意知本题是一个等可能事件的概率，试验发生包含的事件对应的是长度为5的一条线段，
满足条件的事件是组成钝角三角形，包括两种情况
第一种∠ACO为钝角，这种情况的边界是∠ACO=90°的时候，此时OC=1
∴这种情况下，满足要求的0＜OC＜1．
第二种∠OAC为钝角，这种情况的边界是∠OAC=90°的时候，此时OC=4
∴这种情况下，满足要求4＜OC＜5．
综合两种情况，若△AOC为钝角三角形，则0＜OC＜1或4＜OC＜5．
∴概率P=

2

5

=0.4，
（2）△AOC为锐角三角形时，∠ACO为锐角，且∠OAB是锐角
当∠ACO=90°时，有勾股定理求得OC=1，
∠OAC=90°时，由直角三角形中的边角关系，解得OC=4，BC=1
综上，△AOC三个角都是锐角时1＜OC＜4，
其概率为：P=

4-1

5

=0.6．

点评：本题考查等可能事件的概率，几何概型的解法，体现了分类讨论的数学思想．