题目内容
5.已知函数f(x)=$\frac{1}{3}$x3-mx2+x+2有两个极值点,则m的取值范围是( )| A. | (-1,1) | B. | [-1,1] | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-1)∪(1,+∞) |
分析 求出函数的导数,问题转化为导函数f′(x)=0有2个不相等的实数根,根据二次函数的性质求出m的范围即可.
解答 解:f′(x)=x2-2mx+1,
若f(x)在R上有两个极值点,
则f′(x)=0有2个不相等的实数根,
∴△=4m2-4>0,
解得:m>1或m<-1,
故选:D.
点评 本题考查了函数的极值问题,考查导数的应用以及二次函数的性质,是一道基础题.

练习册系列答案
相关题目
16.执行如图所示的程序框图,则输出y的值为( )
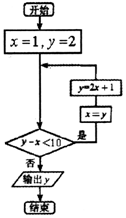

| A. | 5 | B. | 11 | C. | 23 | D. | 47 |
13.如果直线x=ky-1与圆C:x2+y2+kx+my+2p=0相交,且两个交点关于直线y=x对称,那么实数p的取值范围是( )
| A. | $({-∞,-\frac{3}{2}})$ | B. | $({-∞,-\frac{3}{4}})$ | C. | $({-\frac{3}{4},+∞})$ | D. | $({-\frac{3}{2},+∞})$ |
20.数列$-\frac{1}{3}$,$\frac{1}{9}$,-$\frac{1}{27}$,$\frac{1}{81}$,…的一个通项公式可能是( )
| A. | (-1)n-1$\frac{1}{{3}^{n}}$ | B. | (-1)n-1$\frac{1}{3n}$ | C. | (-1)n$\frac{1}{{3}^{n}}$ | D. | (-1)n$\frac{1}{3n}$ |
10.数列{an}的通项an是关于x的不等式x2-x<nx(n∈N*)的解集中的整数个数,则数列{an}的前n项和Sn=( )
| A. | n2 | B. | n(n+1) | C. | $\frac{n(n+1)}{2}$ | D. | (n+1)(n+2) |
3.已知函数f(x)=log3x,x0∈[1,27],则不等式1≤f(x0)≤2成立的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{3}{13}$ | D. | $\frac{2}{9}$ |