题目内容
椭圆
+
=1的焦点坐标是（ ）
| x2 |
| m-2 |
| y2 |
| m+5 |
| A、（±7，0） | ||
| B、（0，±7） | ||
C、（±
| ||
D、（0，±
|
考点：椭圆的标准方程
专题：圆锥曲线的定义、性质与方程
分析：利用椭圆的简单性质求解．
解答：
解：椭圆
+
=1中，
c=
=
，
∴椭圆
+
=1的焦点坐标是（0，±
）．
故选：D．
| x2 |
| m-2 |
| y2 |
| m+5 |
c=
| (m+5)-(m-2) |
| 7 |
∴椭圆
| x2 |
| m-2 |
| y2 |
| m+5 |
| 7 |
故选：D．
点评：本题考查椭圆的焦点坐标的求法，是基础题，解题时要认真审题，注意椭圆的简单性质的灵活运用．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
下列函数中与函数y=x相等的是（ ）
| A、y=x+1 | |||
B、y=
| |||
C、y=
| |||
D、（
|
设数列{an}满足a1=0，an+an+1=2，则a2014的值为（ ）
| A、2 | B、1 | C、0 | D、-2 |
已知A、B、C三点同在直线l上，点O不在l上，且
=（1+xlnx）
-（mx2-f（x））
，又函数f（x）的极大值点为x1，极小值点为x2，则（ ）
| OA |
| OB |
| OC |
A、0＜m＜
| ||
| B、0＜m＜1，x1＜1＜x2 | ||
| C、0＜m＜1，x2＜1＜x1 | ||
D、0＜m＜
|
f（x）=2x+3x的一个零点所在的一个区间是 （ ）
| A、（1，2） |
| B、（0，1） |
| C、（-1，0） |
| D、（-2，-1） |
设双曲线
-y2=1（a＞0）与直线l：x+y=1相交于两个不同点，则双曲线的离心率e的取值范围为（ ）
| x2 |
| a2 |
A、（
| ||||||||
B、（
| ||||||||
C、（
| ||||||||
D、（
|
a＞b＞0，下列不等式一定成立的是（ ）
A、a+
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
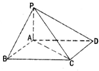如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠ABC=60°，BC=2AB，PA⊥底面ABCD．