题目内容
某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区.B肯定是受A感染的.对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是
.同样也假定D受A、B和C感染的概率都是
.在这种假定之下,B、C、D中直接受A感染的人数x就是一个随机变量.写出x的分布列(不要求写出计算过程),并求x的均值(即数学期望).
| 1 |
| 2 |
| 1 |
| 3 |
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:由题意知X的可能取值为1,2,3,分别求出相应的概率,由此能求出x的分布列和x的均值.
解答:
解:由题意知X的可能取值为1,2,3,
随机变量X的分布列是
X的均值为EX=1×
+2×
+3×
=
.
随机变量X的分布列是
| X | 1 | 2 | 3 | ||||||
| P |
|
|
|
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 11 |
| 6 |
点评:本题考查离散型随机变量的分布列和均值的求法,是中档题,在历年高考中都是必考题型.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
已知A、B、C三点同在直线l上,点O不在l上,且
=(1+xlnx)
-(mx2-f(x))
,又函数f(x)的极大值点为x1,极小值点为x2,则( )
| OA |
| OB |
| OC |
A、0<m<
| ||
| B、0<m<1,x1<1<x2 | ||
| C、0<m<1,x2<1<x1 | ||
D、0<m<
|
 如图,已知长方体ABCD-EFGH中,AB=
如图,已知长方体ABCD-EFGH中,AB=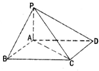 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠ABC=60°,BC=2AB,PA⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠ABC=60°,BC=2AB,PA⊥底面ABCD.