题目内容
17.在面积为$\sqrt{15}$的△ABC中,角A、B、C的对边分别为a、b、c,且c+bsinAtanB=4a+bcosA,sinA=2sinC,则a+c=6.分析 将切化弦,利用两角和差的余弦公式化简,结合a=2c和余弦定理得出b,c的关系,利用三角形的面积列方程解出三角形的边长.
解答 解:∵c+bsinAtanB=4a+bcosA,∴ccosB+bsinAsinB=4acosB+bcosAcosB,
∴(c-4a)cosB=b(cosAcosB-sinAsinB)=bcos(A+B)=-bcosC.
∵sinA=2sinC,∴a=2c,
∴-7ccosB=-bcosC.
∴7c×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=b×$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,即3a2+4c2-4b2=0,
∵a=2c,∴12c2+4c2=4b2,∴b=2c.
∴a=b=2c.
∴△ABC是等腰三角形,设AB边上的高为h,则h=$\sqrt{{a}^{2}-\frac{{c}^{2}}{4}}$=$\frac{\sqrt{15}}{2}c$.
∴S=$\frac{1}{2}ch$=$\frac{1}{2}×c×\frac{\sqrt{15}}{2}c$=$\sqrt{15}$.解得c=2.
∴a+c=3c=6.
故答案为6.
点评 本题考查了正余弦定理,三角函数的恒等变换,属于中档题.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
7.已知集合A={x|(x-4)(x+2)<0},B={-3,-1,1,3,5},则A∩B=( )
| A. | {-1,1,3} | B. | {-3,-1,1,3} | C. | {-1,1,3,5} | D. | {-3,5} |
8.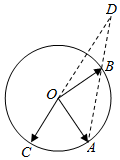 已知A,B,C为圆O上三点,CO的延长线与线段AB的延长线交于圆O外一点D,且|OD|=2|OC|,若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$,则p+q的值为( )
已知A,B,C为圆O上三点,CO的延长线与线段AB的延长线交于圆O外一点D,且|OD|=2|OC|,若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$,则p+q的值为( )
 已知A,B,C为圆O上三点,CO的延长线与线段AB的延长线交于圆O外一点D,且|OD|=2|OC|,若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$,则p+q的值为( )
已知A,B,C为圆O上三点,CO的延长线与线段AB的延长线交于圆O外一点D,且|OD|=2|OC|,若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$,则p+q的值为( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
 已知四边形PQRS是圆内接四边形,∠PSR=90°,过点Q作PR、PS的垂线,垂足分别为点H、K.
已知四边形PQRS是圆内接四边形,∠PSR=90°,过点Q作PR、PS的垂线,垂足分别为点H、K.