题目内容
5. 已知四边形PQRS是圆内接四边形,∠PSR=90°,过点Q作PR、PS的垂线,垂足分别为点H、K.
已知四边形PQRS是圆内接四边形,∠PSR=90°,过点Q作PR、PS的垂线,垂足分别为点H、K.(1)求证:Q、H、K、P四点共圆;
(2)求证:QT=TS.
分析 (1)利用直角三角形的三个顶点可看作以斜边为直径的圆上的三点即得结论;
(2)通过互补、同弧所对的圆周角相等,说明△TSK、△TKQ为等腰三角形即可.
解答 证明:(1)∵过点Q作PR、PS的垂线,垂足分别为点H、K,
∴∠PHQ=∠PKQ=90°,
∴Q、H、K、P四点共圆;
(2)∵Q、H、K、P四点共圆,
∴∠HKS=$\frac{π}{2}$-∠HPQ=∠HQP,①
∵∠PSR=90°,PR为圆B的直径,
∴∠PQR=90°,∠QRH=∠HQP,②
由①②得,∠QSP=∠HKS,
∴△TSK为等腰三角形,ST=TK,
又∵∠SKQ=90°,
∴∠SQK=∠TKQ,即△TKQ为等腰三角形,QT=TK,
∴QT=TS.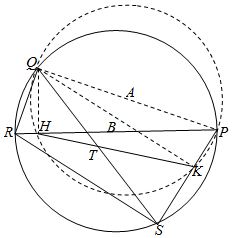
点评 本题考查综合法在证明中的应用,考查数形结合能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
15.设函数y=ax2与函数y=|$\frac{lnx+1}{ax}$|的图象恰有3个不同的交点,则实数a的取值范围为( )
| A. | ($\frac{\sqrt{3}}{3}$e,$\sqrt{e}$) | B. | (-$\frac{\sqrt{3}}{3}$e,0)∪(0,$\frac{\sqrt{3}}{3}$e) | C. | (0,$\frac{\sqrt{3}}{3}$e) | D. | ($\frac{1}{\sqrt{e}}$,1)∪{$\frac{\sqrt{3}}{3}$e} |
16.已知命题p:?x∈R,sinx+cosx=2,q:?x∈R,x2+x+1>0,则下列命题中正确的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |
13.已知角α的顶点为坐标原点,始边为x轴正半轴,终边落在第二象限,A(x,y)是其终边上一点,向量$\overrightarrow{m}$=(3,4),若$\overrightarrow{m}$⊥$\overrightarrow{OA}$,则tan(α+$\frac{π}{4}}$)=( )
| A. | 7 | B. | $-\frac{1}{7}$ | C. | -7 | D. | $\frac{1}{7}$ |
20.已知直线y=m(0<m<2)与函数f(x)=2sin(ωx+φ)(ω>0)的图象相邻的三个交点依次为A(1,m),B(5,m),C(7,m),则ω=( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{6}$ |
10.设p:1<x<2,q:lnx<1,则p是q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |