题目内容
8．
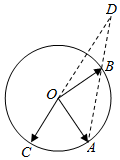已知A，B，C为圆O上三点，CO的延长线与线段AB的延长线交于圆O外一点D，且|OD|=2|OC|，若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$，则p+q的值为（ ）| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | -2 | D． | 2 |
分析 由条件及向量数乘的几何意义便可得出$\overrightarrow{OD}=-2\overrightarrow{OC}$，从而便可得出$\overrightarrow{OD}=-2p\overrightarrow{OA}-2q\overrightarrow{OB}$，而A，B，D三点共线，这样即可得出-2p-2q=1，从而便可求出p+q的值．
解答 解：根据条件，$\overrightarrow{OD}=-2\overrightarrow{OC}$；
又$\overrightarrow{OC}=p\overrightarrow{OA}+q\overrightarrow{OB}$；
∴$\overrightarrow{OD}=-2p\overrightarrow{OA}-2q\overrightarrow{OB}$；
又A，B，D三点共线；
∴-2p-2q=1；
∴$p+q=-\frac{1}{2}$．
故选：A．
点评 考查向量数乘的几何意义，以及向量数乘的运算，A，B，C三点共线的充要条件：$\overrightarrow{OB}=x\overrightarrow{OA}+y\overrightarrow{OC}$，且x+y=1．
练习册系列答案
相关题目
19．已知全集为R，集合M={-1，1，2，4}，N={x|x2-2x＞3}，则M∩（∁RN）=（ ）
| A． | {-1，1，2} | B． | {1，2} | C． | {4} | D． | {x|-1≤x≤2} |
16．已知命题p：?x∈R，sinx+cosx=2，q：?x∈R，x2+x+1＞0，则下列命题中正确的是（ ）
| A． | p∧q | B． | ￢p∧q | C． | p∨（￢q） | D． | （￢p）∧（￢q） |
3．已知函数f（x）=cosωx-sinωx（ω＞0）在（-$\frac{π}{2}$，$\frac{π}{2}$）上单调递减，则ω的取值不可能为（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{4}$ |
13．已知角α的顶点为坐标原点，始边为x轴正半轴，终边落在第二象限，A（x，y）是其终边上一点，向量$\overrightarrow{m}$=（3，4），若$\overrightarrow{m}$⊥$\overrightarrow{OA}$，则tan（α+$\frac{π}{4}}$）=（ ）
| A． | 7 | B． | $-\frac{1}{7}$ | C． | -7 | D． | $\frac{1}{7}$ |
20．已知直线y=m（0＜m＜2）与函数f（x）=2sin（ωx+φ）（ω＞0）的图象相邻的三个交点依次为A（1，m），B（5，m），C（7，m），则ω=（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{2}$ | D． | $\frac{π}{6}$ |
18．已知等差数列{an}的前n项和为Sn，类似地，若ak∈N*，则记${S}_{{a}_{k}}$为等差数列{an}的前ak项和，若${S}_{{a}_{2}}$=9，S2=5，则等差数列{an}的前an项和${S}_{{a}_{n}}$=（ ）
| A． | $\frac{1}{2}$n2+$\frac{5}{2}$n+1 | B． | $\frac{1}{2}$n2+$\frac{1}{2}$n+2 | C． | $\frac{1}{2}$n2+$\frac{5}{2}$n+2 | D． | $\frac{1}{2}$n2+$\frac{3}{2}$n+4 |