题目内容
(文科)一动圆过定点P(0,1),且与定直线l:y=-1相切.
(1)求动圆圆心C的轨迹方程;
(2)若(1)中的轨迹上两动点记为A(x1,y1),B(x2,y2),且x1x2=-16.
①求证:直线AB过一定点,并求该定点坐标;
②求|PA|+|PB|的取值范围.
(1)求动圆圆心C的轨迹方程;
(2)若(1)中的轨迹上两动点记为A(x1,y1),B(x2,y2),且x1x2=-16.
①求证:直线AB过一定点,并求该定点坐标;
②求|PA|+|PB|的取值范围.
考点:圆锥曲线的综合,轨迹方程
专题:圆锥曲线中的最值与范围问题
分析:(1)直接由抛物线的定义得抛物线的方程;
(2)①设出AB所在直线方程y=kx+b,和抛物线方程联立后由根与系数关系结合已知条件求得b的值,则可证得直线过定点,并求得定点坐标;
②由抛物线的定义,结合(2)①中的根与系数关系把|PA|+|PB|转化为含有k的代数式,则|PA|+|PB|的取值范围可求.
(2)①设出AB所在直线方程y=kx+b,和抛物线方程联立后由根与系数关系结合已知条件求得b的值,则可证得直线过定点,并求得定点坐标;
②由抛物线的定义,结合(2)①中的根与系数关系把|PA|+|PB|转化为含有k的代数式,则|PA|+|PB|的取值范围可求.
解答:
(1)解:由已知动圆过定点P(0,1),且与定直线l:y=-1相切,
∴动圆圆心C到点P与到定直线l的距离相等,
∴点C的轨迹是以P为焦点,定直线l为准线的抛物线.
∴所求方程为:x2=4y;
(2)①证明:设直线AB方程为:y=kx+b,
由
,消去y得:x2-4kx-4b=0.
∴x1+x2=4k,x1x2=-4b.
∵x1x2=-16,∴b=4.
∴直线AB过定点(0,4);
②解:由抛物线定义知:|PA|=y1+1,|PB|=y2+1,
又y1=kx1+4,y2=kx2+4,x1+x2=4k,x1x2=-16.
∴|PA|+|PB|=k(x1+x2)+10=4k2+10≥10(等号当k=0时成立),
∴所求|PA|+|PB|的取值范围是[10,+∞).
∴动圆圆心C到点P与到定直线l的距离相等,
∴点C的轨迹是以P为焦点,定直线l为准线的抛物线.
∴所求方程为:x2=4y;
(2)①证明:设直线AB方程为:y=kx+b,
由
|
∴x1+x2=4k,x1x2=-4b.
∵x1x2=-16,∴b=4.
∴直线AB过定点(0,4);
②解:由抛物线定义知:|PA|=y1+1,|PB|=y2+1,
又y1=kx1+4,y2=kx2+4,x1+x2=4k,x1x2=-16.
∴|PA|+|PB|=k(x1+x2)+10=4k2+10≥10(等号当k=0时成立),
∴所求|PA|+|PB|的取值范围是[10,+∞).
点评:本题考查了轨迹方程的求法,考查了直线与圆锥曲线的位置关系,解答直线与圆锥曲线的关系问题,常把直线与圆锥曲线联立,化为关于x的一元二次方程后,利用一元二次方程根与系数的关系求解,是高考试卷中的压轴题.

练习册系列答案
相关题目
一个三棱柱的侧棱垂直于底面,且所有棱长都为a,则此三棱柱的外接球的表面积为( )
| A、πa2 | ||
| B、15πa2 | ||
C、
| ||
D、
|
一项射击实验的标靶为圆形.在子弹命中标靶的前提下,一次射击能够击中标靶的内接正方形的概率是( )
| A、50% | ||
B、
| ||
| C、0.2π | ||
D、
|
将直线2x-y+λ=0沿x轴向左平移一个单位,所得直线与曲线C:
(θ为参数)相切,则实数λ的值为( )
|
| A、-7或3 | B、-2或8 |
| C、0或10 | D、1或11 |
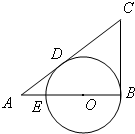 如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则AB的长为
如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则AB的长为 已知函数f(x)=lg(2+x)+lg(2-x).
已知函数f(x)=lg(2+x)+lg(2-x).