题目内容
 已知函数f(x)=lg(2+x)+lg(2-x).
已知函数f(x)=lg(2+x)+lg(2-x).(Ⅰ)求函数y=f(x)的定义域;
(Ⅱ)判断函数y=f(x)的奇偶性;
(Ⅲ)若f(m-2)<f(m),求m的取值范围.
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(Ⅰ)由
,求得x的范围,可得函数y=f(x)定义域.
(Ⅱ)由于函数y=f(x)的定义域关于原点对称.且满足 f(-x)=f(x),可得函数y=f(x)为偶函数.
(Ⅲ)化简函数f(x)的解析式为lg(4-x2),结合函数的单调性可得,不等式f(m-2)<f(m)等价于|m|<|m-2|<2,由此求得m的范围.
|
(Ⅱ)由于函数y=f(x)的定义域关于原点对称.且满足 f(-x)=f(x),可得函数y=f(x)为偶函数.
(Ⅲ)化简函数f(x)的解析式为lg(4-x2),结合函数的单调性可得,不等式f(m-2)<f(m)等价于|m|<|m-2|<2,由此求得m的范围.
解答:
解:(Ⅰ)要使函数有意义,则
,解得-2<x<2,
故函数y=f(x)定义域为(-2,2).
(Ⅱ)由(Ⅰ)可知,函数y=f(x)的定义域为(-2,2),关于原点对称.
对任意x∈(-2,2),则-x∈(-2,2),
∵f(-x)=lg(2-x)+lg(2+x)=f(x),
∴由函数奇偶性可知,函数y=f(x)为偶函数.
(Ⅲ)∵函数f(x)=lg(2+x)+lg(2-x)=lg(4-x2),
由复合函数单调性判断法则知,当0≤x<2时,函数y=f(x)为减函数.
又函数y=f(x)为偶函数,
∴不等式f(m-2)<f(m)等价于|m|<|m-2|<2,
解得0<m<1.
|
故函数y=f(x)定义域为(-2,2).
(Ⅱ)由(Ⅰ)可知,函数y=f(x)的定义域为(-2,2),关于原点对称.
对任意x∈(-2,2),则-x∈(-2,2),
∵f(-x)=lg(2-x)+lg(2+x)=f(x),
∴由函数奇偶性可知,函数y=f(x)为偶函数.
(Ⅲ)∵函数f(x)=lg(2+x)+lg(2-x)=lg(4-x2),
由复合函数单调性判断法则知,当0≤x<2时,函数y=f(x)为减函数.
又函数y=f(x)为偶函数,
∴不等式f(m-2)<f(m)等价于|m|<|m-2|<2,
解得0<m<1.
点评:本题主要考查求函数的定义域,函数的奇偶性的判断,复合函数的单调性,属于中档题.

练习册系列答案
相关题目
一个几何体的三视图如图所示,这个几何体可能是一个( )
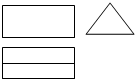

| A、三棱锥 |
| B、底面不规则的四棱锥 |
| C、三棱柱 |
| D、底面为正方形的四棱锥 |
经过两点A(4,2y+1),B(2,-3)的直线的倾斜角为
,则y=( )
| 3π |
| 4 |
| A、-1 | B、0 | C、-3 | D、2 |
已知集合A={x||x|<3},B={x|x-2≤0},则A∪B等( )
| A、(-∞,3] |
| B、(-∞,3) |
| C、[2,3) |
| D、(-3,2] |
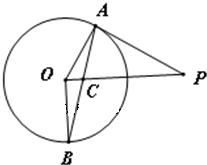 如图,已知PA与圆O相切于点A,OB⊥OP,AB交PO与点C.
如图,已知PA与圆O相切于点A,OB⊥OP,AB交PO与点C. 在边长为10的正方形ABCD内有一动点P,AP=9,作PQ⊥BC于Q,PR⊥CD于R,求矩形PQCR面积的最小值和最大值,并指出取最大值时P的具体位置.
在边长为10的正方形ABCD内有一动点P,AP=9,作PQ⊥BC于Q,PR⊥CD于R,求矩形PQCR面积的最小值和最大值,并指出取最大值时P的具体位置.