题目内容
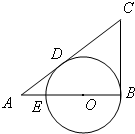 如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则AB的长为
如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则AB的长为考点:与圆有关的比例线段
专题:立体几何
分析:利用切割线定理可得AD2=AE•AB,即可得出AB,再利用切线的判定与切线长定理可得CB=CD,再利用勾股定理即可得出.
解答:
解:∵AD是⊙O是切线,
∴AD2=AE•AB.
∵AD=2,AE=1.
∴22=1×AB,解得AB=4.
∵∠B=90°,
∴AC2=AB•BC.
∴(2+CD)2=42+BC2,
∵∠B=90°,AB是⊙O的直径,
∴CB是⊙O的切线.
∴CD=CB,
∴(2+CD)2=42+CD2,解得CD=3.
故答案分别为:4,3.
∴AD2=AE•AB.
∵AD=2,AE=1.
∴22=1×AB,解得AB=4.
∵∠B=90°,
∴AC2=AB•BC.
∴(2+CD)2=42+BC2,
∵∠B=90°,AB是⊙O的直径,
∴CB是⊙O的切线.
∴CD=CB,
∴(2+CD)2=42+CD2,解得CD=3.
故答案分别为:4,3.
点评:本题考查了圆的切割线定理、切线的判定与性质定理、切线长定理、勾股定理,属于基础题.

练习册系列答案
相关题目
函数f(x)=
( )
| 2x-2-x |
| 3 |
| A、是奇函数,在(-∞,+∞)上是增函数 |
| B、是偶函数,在(-∞,+∞)上是减函数 |
| C、是偶函数,在(-∞,+∞)上是增函数 |
| D、是奇函数,在(-∞,+∞)上是减函数 |
已知受限制的二次函数y=f(x),x∈[-1,2],f(0)=2,f(1)=0,f(
)=
,则该函数的值域为( )
| 1 |
| 2 |
| 3 |
| 4 |
| A、[0,6] | ||
B、[-
| ||
C、[-
| ||
D、(-
|
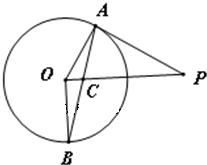 如图,已知PA与圆O相切于点A,OB⊥OP,AB交PO与点C.
如图,已知PA与圆O相切于点A,OB⊥OP,AB交PO与点C.