题目内容
已知f(x)=2cos(
-x)cosx-
cos2x,x∈R,
(1)求f(
)的值;
(2)当x∈[0,
]时,求f(x)的最值.
| π |
| 2 |
| 3 |
(1)求f(
| π |
| 6 |
(2)当x∈[0,
| π |
| 2 |
考点:三角函数中的恒等变换应用
专题:三角函数的求值
分析:(1)利用二倍角公式、辅助角公式化简函数,代入计算,即可求f(
)的值;
(2)当x∈[0,
]时,2x-
∈[-
,
],利用正弦函数的性质,即可求f(x)的最值.
| π |
| 6 |
(2)当x∈[0,
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
解答:
解:(1)∵f(x)=2sinxcosx-
cos2x=sin2x-
cos2x=2sin(2x-
),
∴f(
)=2sin(2•
-
)=0;
(2)∵x∈[0,
]时,
∴2x-
∈[-
,
],
∴sin(2x-
)∈[-
,1],
∴2sin(2x-
)∈[-
,2],
∴f(x)max=2,f(x)min=-
.
| 3 |
| 3 |
| π |
| 3 |
∴f(
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
(2)∵x∈[0,
| π |
| 2 |
∴2x-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴sin(2x-
| π |
| 3 |
| ||
| 2 |
∴2sin(2x-
| π |
| 3 |
| 3 |
∴f(x)max=2,f(x)min=-
| 3 |
点评:本题考查三角函数的化简,考查三角函数的性质,考查学生的计算能力,正确化简函数是关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
已知点P是圆C:x2+y2+4x+ay-5=0上任意一点,P点关于直线2x+y-1=0的对称点在圆上,则实数a等于( )
| A、10 | B、-10 |
| C、20 | D、-20 |
一个几何体的三视图如图所示,这个几何体可能是一个( )
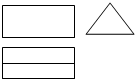

| A、三棱锥 |
| B、底面不规则的四棱锥 |
| C、三棱柱 |
| D、底面为正方形的四棱锥 |
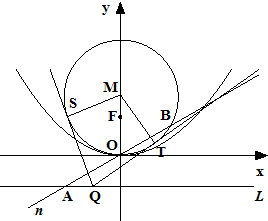 已知抛物线C:x2=2py(p>0)的准线为L,焦点为F,⊙M的圆心在y轴的正半轴上,且与x轴相切,过原点作倾斜角为
已知抛物线C:x2=2py(p>0)的准线为L,焦点为F,⊙M的圆心在y轴的正半轴上,且与x轴相切,过原点作倾斜角为