题目内容
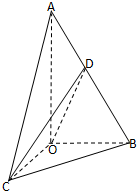 如图,在三棱锥A-BOC中,∠OAB=30°,AO⊥平面BOC,AB=4,∠BOC=90°,BO=CO,D是AB的中点.
如图,在三棱锥A-BOC中,∠OAB=30°,AO⊥平面BOC,AB=4,∠BOC=90°,BO=CO,D是AB的中点.(1)求证:CO⊥平面AOB;
(2)求异面直线AO与CD所成角的正切值.
考点:异面直线及其所成的角,直线与平面垂直的判定
专题:空间角
分析:(1)由已知条件推导出CO⊥AO,CO⊥BO,由此能证明CO⊥平面AOB.
(2)作DE⊥OB,垂足为E,连结CE,则DE∥AO,所以∠CDE是异面直线AO与CD所成的角,由此能求出异面直线AO与CD所成角的正切值.
(2)作DE⊥OB,垂足为E,连结CE,则DE∥AO,所以∠CDE是异面直线AO与CD所成的角,由此能求出异面直线AO与CD所成角的正切值.
解答:
 解:(1)∵AO⊥平面BOC,
解:(1)∵AO⊥平面BOC,
又CO?平面COB,∴CO⊥AO,…(3分)
∵∠BOC=90°,∴CO⊥BO,…(4分)
又∵AO∩B0=O,∴CO⊥平面AOB.…(6分)
(2)作DE⊥OB,垂足为E,连结CE(如图),
则DE∥AO,
∴∠CDE是异面直线AO与CD所成的角.…(8分)
在Rt△COE中,CO=BO=2,OE=
BO=1,
∴CE=
=
.…(10分)
又DE=
AO=
.
∴在Rt△CDE中,tan∠CDE=
=
=
.…(13分)
∴异面直线AO与CD所成角的正切值为
.…(14分)
 解:(1)∵AO⊥平面BOC,
解:(1)∵AO⊥平面BOC,又CO?平面COB,∴CO⊥AO,…(3分)
∵∠BOC=90°,∴CO⊥BO,…(4分)
又∵AO∩B0=O,∴CO⊥平面AOB.…(6分)
(2)作DE⊥OB,垂足为E,连结CE(如图),
则DE∥AO,
∴∠CDE是异面直线AO与CD所成的角.…(8分)
在Rt△COE中,CO=BO=2,OE=
| 1 |
| 2 |
∴CE=
| CO2+OE2 |
| 5 |
又DE=
| 1 |
| 2 |
| 3 |
∴在Rt△CDE中,tan∠CDE=
| CE |
| DE |
| ||
|
| ||
| 3 |
∴异面直线AO与CD所成角的正切值为
| ||
| 3 |
点评:本题考查直线与平面垂直的证明,考查异面直线所成角的正切值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
若a>b,c>d>0,则下列不等式成立的是( )
| A、ac>bd | ||||
B、
| ||||
| C、a+d>b+c | ||||
| D、a-d>b-c |
已知a,x∈R,a≤x4-4x3+4x2+1恒成立,则a的最大值为( )
| A、0 | B、1 | C、2 | D、3 |
在△ABC中,角A、B、C的对边分别为a、b、c,且b+c=2ccos2
,则△ABC是( )
| A |
| 2 |
| A、直角三角形 |
| B、锐角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
收集一只棉铃虫的产卵数y与温度X的几组数据后发现两个变量有相关关系,并按不同的曲线来拟合y与X之间的回归方程,算出对应相关指数R2如下表:
则这组数据模型的回归方程的最好选择应是( )
则这组数据模型的回归方程的最好选择应是( )
| 拟合曲线 | 直 线 | 指数曲线 | 抛 物 线 | 二次曲线 | ||||||||||
| y与x回归方程 |
|
|
|
| ||||||||||
| 相关指数R2 | 0.746 | 0.996 | 0.902 | 0.002 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|