题目内容
设数列{an}是由集合{3s+3t|0≤s＜t，且s，t∈Z}中所有的数从小到大排列成的数列，即a1=4，a2=10，a3=12，a4=28，a5=30，a6=36，…，若a2014=3m+3n（0≤m＜n，且m，n∈Z}，则m+n的值等于 ．
考点：数列递推式
专题：综合题,等差数列与等比数列
分析：如果用（t，s）表示3s+3t，分别根据数列an的值，确定an的利取值规律，利用归纳推理即可得到结论．
解答：
解：如果用（t，s）表示3s+3t，
则a1=（0，1）=30+31，a2=（0，2）=30+32，
a3=（1，2）=31+32，a4=（0，3），
a5=（1，3），a6=（2，3），
a7=（0，4），a8=（1，4），
a9=（2，4），a10=（3，4）．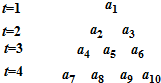
利用归纳推理即可得：
…，
当t=62时，最后一项为1+2+…+62=
=1953，
当t=63时，最后一项为1+2+…+63=
=2016，
∴a2014一定在第63行，则a2016=（62，63），向前数三个即是a2013，
∴a2013=（60，63）
即m=60，n=63，
∴m+n=60+63=123，
故答案为：123
则a1=（0，1）=30+31，a2=（0，2）=30+32，
a3=（1，2）=31+32，a4=（0，3），
a5=（1，3），a6=（2，3），
a7=（0，4），a8=（1，4），
a9=（2，4），a10=（3，4）．
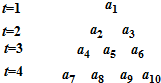
利用归纳推理即可得：
…，
当t=62时，最后一项为1+2+…+62=
| 62×63 |
| 2 |
当t=63时，最后一项为1+2+…+63=
| 63×64 |
| 2 |
∴a2014一定在第63行，则a2016=（62，63），向前数三个即是a2013，
∴a2013=（60，63）
即m=60，n=63，
∴m+n=60+63=123，
故答案为：123
点评：本题考查了一个探究规律型的问题，解题时要认真分析题意，寻找其中的规律，从而解出结果．综合性较强，难度较大．
练习册系列答案
名校课堂系列答案
相关题目
某程序框图如右图所示，则输出的n值是（ ）
| A、.21 | B、22 |
| C、．23 | D、．24 |
设集合A={-1，0，1，2}，B={-1，2，3}，则A∩B=（ ）
| A、{-1，0，1，2，3} |
| B、{-1，2} |
| C、{0，1，3} |
| D、{x|-1≤x≤2} |