题目内容
16.已知i是虚数单位,若z(2-i)=2+4i,则复数z=2i.分析 由z(2-i)=2+4i,得$z=\frac{2+4i}{2-i}$,然后利用复数代数形式的乘除运算化简复数z即可得答案.
解答 解:由z(2-i)=2+4i,
得$z=\frac{2+4i}{2-i}$=$\frac{(2+4i)(2+i)}{(2-i)(2+i)}=\frac{10i}{5}=2i$,
故答案为:2i.
点评 本题考查了复数代数形式的乘除运算,是基础题.

练习册系列答案
相关题目
11.设x∈R,则“x>2”是“|x-1|>1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.已知定义在R上的奇函数f(x)满足:当x≥0时,f(x)=x3,若不等式f(-4t)>f(2m+mt2)对任意实数t恒成立,则实数m的取值范围是( )
| A. | (-∞,-$\sqrt{2}$) | B. | (-$\sqrt{2}$,0) | C. | (-∞,0)∪($\sqrt{2}$,+∞) | D. | (-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞) |
5.在(x-2)10展开式中,二项式系数的最大值为 a,含x7项的系数为b,则$\frac{b}{a}$=( )
| A. | $\frac{80}{21}$ | B. | $\frac{21}{80}$ | C. | $-\frac{21}{80}$ | D. | $-\frac{80}{21}$ |
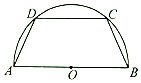 如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.设∠DAB=θ(0<θ<$\frac{π}{2}$),L为等腰梯形ABCD的周长.
如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.设∠DAB=θ(0<θ<$\frac{π}{2}$),L为等腰梯形ABCD的周长.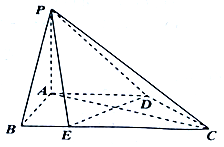 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,AD∥BC,AD=$\frac{1}{2}$BC=2,E在BC上,且BE=$\frac{1}{2}$AB=1,侧棱PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,AD∥BC,AD=$\frac{1}{2}$BC=2,E在BC上,且BE=$\frac{1}{2}$AB=1,侧棱PA⊥平面ABCD.