题目内容
已知函数f(x)=
ax2+2x+(2-a)lnx
(1)当a=-2时,求f(x)的最大值
(2)若在函数f(x)的定义域内存在区间D,使得该函数在区间D上为减函数,求a的取值范围
(3)若曲线C:y=f(x)在点x=1处的切线l与C有且只有一个公共点,求a的值.
| 1 |
| 2 |
(1)当a=-2时,求f(x)的最大值
(2)若在函数f(x)的定义域内存在区间D,使得该函数在区间D上为减函数,求a的取值范围
(3)若曲线C:y=f(x)在点x=1处的切线l与C有且只有一个公共点,求a的值.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)当a=-2时,f(x)=-x2+2x+4lnx,(x>0),f′(x)=
,利用导数研究其单调性极值与最值即可得出;
(2)f′(x)=ax+2+
=
,(x∈(0,+∞)).由于在函数f(x)的定义域内存在区间D,使得该函数在区间D上为减函数,
可得f′(x)≤0在x∈(0,+∞)的一个子集D上成立.即ax≤a-2在x∈(0,+∞)的一个子集D上成立.对a分类讨论即可得出.
(3)f′(1)=4,f(1)=
a+2.可得切线方程y=4x+
a-2,由于曲线C:y=f(x)在点x=1处的切线l与C有且只有一个公共点,因此方程4x+
a-2=
ax2+2x+(2-a)lnx只有一个实数根,令g(x)=
ax2-2x+(2-a)lnx-
a+2,利用导数研究函数的单调性极值即可得出.
| -2(x+1)(x-2) |
| x |
(2)f′(x)=ax+2+
| 2-a |
| x |
| (ax+2-a)(x+1) |
| x |
可得f′(x)≤0在x∈(0,+∞)的一个子集D上成立.即ax≤a-2在x∈(0,+∞)的一个子集D上成立.对a分类讨论即可得出.
(3)f′(1)=4,f(1)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)当a=-2时,f(x)=-x2+2x+4lnx,(x>0),
f′(x)=-2x+2+
=
,令f′(x)>0,解得0<x<2,此时函数f(x)单调递增;令f′(x)<0,解得2<x,此时函数f(x)单调递减.
∴当x=2时,函数f(x)取得最大值f(2)=4ln2.
(2)f′(x)=ax+2+
=
,(x∈(0,+∞)).
∵在函数f(x)的定义域内存在区间D,使得该函数在区间D上为减函数,
∴f′(x)≤0在x∈(0,+∞)的一个子集D上成立.
∴ax≤a-2在x∈(0,+∞)的一个子集D上成立.
若a<0,则x≥1-
,满足题意.
若a>2,则0<x≤1-
,满足题意.
则当0≤a≤2时,不满足题意.
综上可得:a的取值范围是a<0或a>2.
(3)f′(1)=4,f(1)=
a+2.
切线方程为y-
a-2=4(x-1),化为y=4x+
a-2,
∵曲线C:y=f(x)在点x=1处的切线l与C有且只有一个公共点,
∴方程4x+
a-2=
ax2+2x+(2-a)lnx只有一个实数根,
即
ax2-2x+(2-a)lnx-
a+2=0只有一个实数根,
令g(x)=
ax2-2x+(2-a)lnx-
a+2,
g′(x)=ax-2+
=
,
当a=1时,g′(x)=
≥0恒成立,此时函数g(x)单调递增,而g(1)=0,只有一解,满足题意.
当a≠1时,函数g(x)由极值点,其实数根不唯一,因此不满足题意.
∴a=1.
f′(x)=-2x+2+
| 4 |
| x |
| -2(x+1)(x-2) |
| x |
∴当x=2时,函数f(x)取得最大值f(2)=4ln2.
(2)f′(x)=ax+2+
| 2-a |
| x |
| (ax+2-a)(x+1) |
| x |
∵在函数f(x)的定义域内存在区间D,使得该函数在区间D上为减函数,
∴f′(x)≤0在x∈(0,+∞)的一个子集D上成立.
∴ax≤a-2在x∈(0,+∞)的一个子集D上成立.
若a<0,则x≥1-
| 2 |
| a |
若a>2,则0<x≤1-
| 2 |
| a |
则当0≤a≤2时,不满足题意.
综上可得:a的取值范围是a<0或a>2.
(3)f′(1)=4,f(1)=
| 1 |
| 2 |
切线方程为y-
| 1 |
| 2 |
| 1 |
| 2 |
∵曲线C:y=f(x)在点x=1处的切线l与C有且只有一个公共点,
∴方程4x+
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
令g(x)=
| 1 |
| 2 |
| 1 |
| 2 |
g′(x)=ax-2+
| 2-a |
| x |
| (ax-2+a)(x-1) |
| x |
当a=1时,g′(x)=
| (x-1)2 |
| x |
当a≠1时,函数g(x)由极值点,其实数根不唯一,因此不满足题意.
∴a=1.
点评:本题考查了利用导数研究函数的单调性极值与最值、几何意义、切线方程,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
下列函数中,是偶函数且在区间(0,+∞)上单调递增的是( )
| A、y=-ln|x| |
| B、y=x|x| |
| C、y=-x2 |
| D、y=10|x| |
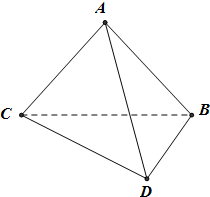 如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.
如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.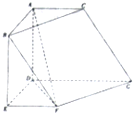 在如图所示的几何体中,四边形ABED是矩形,四边形ADGC是梯形,AD⊥平面DEFG,EF∥DG,∠EDG=120°.
在如图所示的几何体中,四边形ABED是矩形,四边形ADGC是梯形,AD⊥平面DEFG,EF∥DG,∠EDG=120°.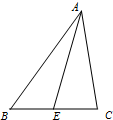 如图,在△ABC中,∠BAC=
如图,在△ABC中,∠BAC=