题目内容
(1)如果log
|x-
|≥log
那么sinx的取值范围是 ;
(2)如果函数f(x)=ax(ax-3a2-1)(a>0且a≠1)在区间[0,+∞)上是增函数,那么实数a的取值
范围是 .
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 2 |
(2)如果函数f(x)=ax(ax-3a2-1)(a>0且a≠1)在区间[0,+∞)上是增函数,那么实数a的取值
范围是
考点:复合函数的单调性
专题:函数的性质及应用
分析:(1)根据对数函数的单调性结合绝对值不等式的解法即可得到结论.
(2)利用换元法结合复合函数单调性之间的关系即可得到结论.
(2)利用换元法结合复合函数单调性之间的关系即可得到结论.
解答:
解:(1)如果log
|x-
|≥log
,则0<|x-
|≤
,
即-
≤x-
≤
且x≠
,
即-
≤x≤
且x≠
,
则-
≤x≤
且x≠
,
-
≤sinx≤1;
(2)设t=ax,则函数f(x)=ax(ax-3a2-1)等价为y=t(t-3a2-1)=t2-(3a2+1)t,
若a>1,当x≥0时,t≥1,
若f(x)(a>0且a≠1)在区间[0,+∞)上是增函数,
则等价为y=t(t-3a2-1)=t2-(3a2+1)t在[1,+∞)上为增函数,即-
=
≤1,
即3a2+1≤2,a2≤
,此时不成立,
若0<a<1,当x≥0时,0<t<1,
若f(x)(a>0且a≠1)在区间[0,+∞)上是增函数,
则等价为y=t(t-3a2-1)=t2-(3a2+1)t在(0,1)上为减函数,即-
=
≤1,
即3a2+1≤2,a2≤
,此时0≤a≤
成立,
故实数a的取值范围是 0≤a≤
.
故答案为:-
≤sinx≤1,0≤a≤
.
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
即-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
即-
| π |
| 6 |
| 5π |
| 6 |
| π |
| 3 |
则-
| π |
| 6 |
| 5π |
| 6 |
| π |
| 3 |
-
| 1 |
| 2 |
(2)设t=ax,则函数f(x)=ax(ax-3a2-1)等价为y=t(t-3a2-1)=t2-(3a2+1)t,
若a>1,当x≥0时,t≥1,
若f(x)(a>0且a≠1)在区间[0,+∞)上是增函数,
则等价为y=t(t-3a2-1)=t2-(3a2+1)t在[1,+∞)上为增函数,即-
| -(3a2+1) |
| 2 |
| 3a2+1 |
| 2 |
即3a2+1≤2,a2≤
| 1 |
| 3 |
若0<a<1,当x≥0时,0<t<1,
若f(x)(a>0且a≠1)在区间[0,+∞)上是增函数,
则等价为y=t(t-3a2-1)=t2-(3a2+1)t在(0,1)上为减函数,即-
| -(3a2+1) |
| 2 |
| 3a2+1 |
| 2 |
即3a2+1≤2,a2≤
| 1 |
| 3 |
| ||
| 3 |
故实数a的取值范围是 0≤a≤
| ||
| 3 |
故答案为:-
| 1 |
| 2 |
| ||
| 3 |
点评:本题主要考查对数不等式的求解以及复合函数单调性的应用,利用换元法结合一元二次函数的性质是解决本题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
下列函数中,是偶函数且在区间(0,+∞)上单调递增的是( )
| A、y=-ln|x| |
| B、y=x|x| |
| C、y=-x2 |
| D、y=10|x| |
若复数z满足(1-3i)z=10i,则z等于( )
| A、-1-3i | B、3-i |
| C、1+3i | D、-3+i |
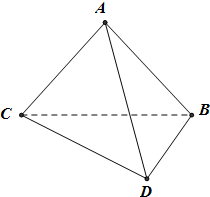 如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.
如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.