题目内容
设0<θ<
,向量
=(sin2θ,cosθ),
=(cosθ,1),若
∥
,则tanθ= .
| π |
| 2 |
| a |
| b |
| a |
| b |
考点:平面向量共线(平行)的坐标表示
专题:平面向量及应用
分析:利用向量共线定理、倍角公式、同角三角函数基本关系式即可得出.
解答:
解:∵
∥
,向量
=(sin2θ,cosθ),
=(cosθ,1),
∴sin2θ-cos2θ=0,
∴2sinθcosθ=cos2θ,
∵0<θ<
,∴cosθ≠0.
∴2tanθ=1,
∴tanθ=
.
故答案为:
.
| a |
| b |
| a |
| b |
∴sin2θ-cos2θ=0,
∴2sinθcosθ=cos2θ,
∵0<θ<
| π |
| 2 |
∴2tanθ=1,
∴tanθ=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了向量共线定理、倍角公式、同角三角函数基本关系式,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设z=
,则z的共轭复数为( )
| 10i |
| 3+i |
| A、-1+3i | B、-1-3i |
| C、1+3i | D、1-3i |
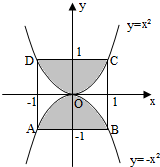 正方形的四个顶点A(-1,-1),B(1,-1),C(1,1),D(-1,1)分别在抛物线y=-x2和y=x2上,如图所示,若将一个质点随机投入正方形ABCD中,则质点落在图中阴影区域的概率是
正方形的四个顶点A(-1,-1),B(1,-1),C(1,1),D(-1,1)分别在抛物线y=-x2和y=x2上,如图所示,若将一个质点随机投入正方形ABCD中,则质点落在图中阴影区域的概率是