题目内容
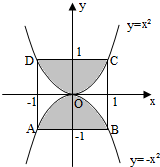 正方形的四个顶点A(-1,-1),B(1,-1),C(1,1),D(-1,1)分别在抛物线y=-x2和y=x2上,如图所示,若将一个质点随机投入正方形ABCD中,则质点落在图中阴影区域的概率是
正方形的四个顶点A(-1,-1),B(1,-1),C(1,1),D(-1,1)分别在抛物线y=-x2和y=x2上,如图所示,若将一个质点随机投入正方形ABCD中,则质点落在图中阴影区域的概率是考点:几何概型
专题:概率与统计
分析:利用几何槪型的概率公式,求出对应的图形的面积,利用面积比即可得到结论.
解答:
解:∵A(-1,-1),B(1,-1),C(1,1),D(-1,1),
∴正方体的ABCD的面积S=2×2=4,
根据积分的几何意义以及抛物线的对称性可知阴影部分的面积S=2
(1-x2)dx=2(x-
x3)
=2[(1-
)-(-1+
)]=2×
=
,
则由几何槪型的概率公式可得质点落在图中阴影区域的概率是
=
.
故答案为:
.
∴正方体的ABCD的面积S=2×2=4,
根据积分的几何意义以及抛物线的对称性可知阴影部分的面积S=2
| ∫ | 1 -1 |
| 1 |
| 3 |
| | | 1 -1 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
则由几何槪型的概率公式可得质点落在图中阴影区域的概率是
| ||
| 4 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题主要考查几何槪型的概率的计算,利用积分求出阴影部分的面积是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
从正方形四个顶点及其中心这5个点中,任取2个点,则这2个点的距离不小于该正方形边长的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
阅读如图的程序框图,运行相应的程序,输出S的值为( )


| A、15 | B、105 |
| C、245 | D、945 |
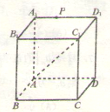 如图,P是正方体ABCD-A1B1C1D1棱A1D1上一点,设点P和直线AC1确定的平面为α,过点P与直线AC1垂直的平面为β,则下列命题正确的是
如图,P是正方体ABCD-A1B1C1D1棱A1D1上一点,设点P和直线AC1确定的平面为α,过点P与直线AC1垂直的平面为β,则下列命题正确的是