设椭圆C:x2a2+y2b2=1的左右焦点为F1.F2.过F2作x轴的垂线与C相交于A.B两点.F1B与y轴相交于点D.若AD⊥F1B.则椭圆C的离心率等于．题目和参考答案——青夏教育精英家教网—

题目内容

设椭圆C：

=1（a＞b＞0）的左右焦点为F₁，F₂，过F₂作x轴的垂线与C相交于A，B两点，F₁B与y轴相交于点D，若AD⊥F₁B，则椭圆C的离心率等于

．

考点：椭圆的简单性质

专题：圆锥曲线的定义、性质与方程

分析：根据条件分别求出A，B，D的坐标，利用AD⊥F₁B，建立方程关系即可得到结论．

解答：

解：连接AF₁，∵OD∥AB，O为F₁F₂的中点，
∴D为BF₁的中点，
又AD⊥BF₁，∴|AF₁|=|AB|．
∴|AF₁|=2|AF₂|．
设|AF₂|=n，则|AF₁|=2n，|F₁F₂|=

n，
∴e=

|F1F2|

|AF1|+|AF2|

．

点评：本题主要考查椭圆离心率的求解，根据条件求出对应点的坐标，利用直线垂直与斜率之间的关系是解决本题的关键，运算量较大．为了方便，可以先确定一个参数的值．

练习册系列答案

△ABC的内角A，B，C所对应的边分别为a，b，c．
（Ⅰ）若a，b，c成等差数列，证明：sinA+sinC=2sin（A+C）；
（Ⅱ）若a，b，c成等比数列，求cosB的最小值．

根据世行2013年新标准，人均GDP低于1035美元为低收入国家；人均GDP为1035-4085美元为中等偏下收入国家；人均GDP为4085-12616美元为中等偏上收入国家；人均GDP不低于12616美元为高收入国家．某城市有5个行政区，各区人口占该城市人口比例及人均GDP如下表：

行政区	区人口占城市人口比例	区人均GDP（单位：美元）
A	25%	8000
B	30%	4000
C	15%	6000
D	10%	3000
E	20%	10000

（Ⅰ）判断该城市人均GDP是否达到中等偏上收入国家标准；
（Ⅱ）现从该城市5个行政区中随机抽取2个，求抽到的2个行政区人均GDP都达到中等偏上收入国家标准的概率．

如图，在平行四边形ABCD中，已知AB=8，AD=5，

．

，x≥0，若f₁（x）=f（x），f_n+1（x）=f（f_n（x）），n∈N₊，则f₂₀₁₄（x）的表达式为

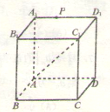如图，P是正方体ABCD-A₁B₁C₁D₁棱A₁D₁上一点，设点P和直线AC₁确定的平面为α，过点P与直线AC₁垂直的平面为β，则下列命题正确的是

①存在平面α，使得A₁B∥α；
②对任意平面α都有α⊥β；
③平面α将正方体分割为体积相等的两部分；
④β截正方体所得截面多边形可能是四边形．

在平面直角坐标系中，O为原点，A（-1，0），B（0，

试题分类