题目内容
14.已知P(t,t),t∈R,点M是圆O1:x2+(y-1)2=$\frac{1}{4}$上的动点,点N是圆O2:(x-2)2+y2=$\frac{1}{4}$上的动点,求PN-PM的最大值.分析 先根据两圆的方程求出圆心和半径,结合图形,把求PN-PM的最大值转化为PO2-PO1+1的最大值,
再利用PO2-PO1=PO2-PO1′≤O1′O2=1,即可求出对应的最大值.
解答 解:如图所示,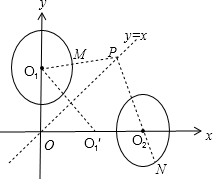
圆O1:x2+(y-1)2=$\frac{1}{4}$的圆心O1(0,1),
圆O2:(x-2)2+y2=$\frac{1}{4}$的圆心O2(2,0),这两个圆的半径都是$\frac{1}{2}$;
要使PN-PM最大,需PN最大,且PM最小,
由图可得,PN最大值为PO2+$\frac{1}{2}$,
PM的最小值为PO1-$\frac{1}{2}$,
故PN-PM最大值是(PO2+$\frac{1}{2}$)-(PO1-$\frac{1}{2}$)=PO2-PO1+1,
点P(t,t)在直线 y=x上,O1(0,1)关于y=x的对称点O1′(1,0),
直线O2O1′与y=x的交点为原点O,
则PO2-PO1=PO2-PO1′≤O1′O2=1,
故PO2-PO1+1的最大值为1+1=2,
即PN-PM的最大值为2.
点评 本题考查了直线与圆的方程的综合应用问题,主要考查圆的标准方程,点与圆的位置关系,体现了转化及数形结合的数学思想,是综合性题目.

练习册系列答案
相关题目
4.一个几何体三视图如图,则该几何体的表面积为( )


| A. | 6 | B. | 7 | C. | 6+$\sqrt{2}$ | D. | 7+$\sqrt{2}$ |
5.已知命题P:“若b2=ac(a,b,c∈R),则a,b,c成等比数列”,q:“函数f(x)=cos($\frac{π}{2}$+x)是奇函数”,则下列命题为真命题的是( )
| A. | p∨q | B. | p∧q | C. | p∨¬q | D. | ¬p∧¬q |