题目内容
函数f(x)=
ln
的图象可能是( )
| 1 |
| 3 |
| 1+x |
| 1-x |
A、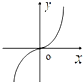 |
B、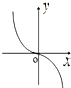 |
C、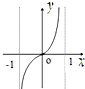 |
D、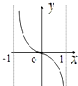 |
考点:函数的图象
专题:函数的性质及应用
分析:根据函数是奇函数,图象关于原点对称,求出定义域为(-1,1),且函数f(x)在(-1,1)上是减函数,由此得出结论.
解答:
解:由于函数f(-x)=
ln
=-
ln
=-f(x),故函数f(x)=
ln
是奇函数,图象关于原点对称.
由
>0 解得-1<x<1,故函数的定义域为(-1,1).
再由函数f(x)=
ln
=
ln[
-1],函数g(x)=
在(-1,1)上是增函数,故函数f(x)在定义域(-1,1)上是增函数,
故选C.
| 1 |
| 3 |
| 1-x |
| 1+x |
| 1 |
| 3 |
| 1+x |
| 1-x |
| 1 |
| 3 |
| 1+x |
| 1-x |
由
| 1+x |
| 1-x |
再由函数f(x)=
| 1 |
| 3 |
| 1+x |
| 1-x |
| 1 |
| 3 |
| 2 |
| 1-x |
| 2 |
| 1-x |
故选C.
点评:本题主要考查函数的单调性和奇偶性的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在有限数列{an}中,Sn是{an}的前n项和,若把
称为数列{an}的“优化和”,现有一个共2006项的数列{an}:a1,a2,a3,…,a2006,若其“优化和”为2007,则有2007项的数列1,a1,a2,a3,…,a2006的“优化和”为( )
| S1+S2+S3+…+Sn |
| n |
| A、2005 | B、2006 |
| C、2007 | D、2008 |
已知函数g(x)=2x-1,函数y=f(x)是y=g(x)的反函数,设a>b>c>0,则
,
,
的大小关系为( )
| f(a) |
| a |
| f(b) |
| b |
| f(c) |
| c |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
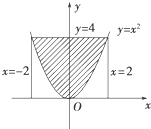 如图在区域Ω={(x,y)|-2≤x≤2,0≤y≤4}中随机撒豆子,豆子落在图中阴影部分内的概率为
如图在区域Ω={(x,y)|-2≤x≤2,0≤y≤4}中随机撒豆子,豆子落在图中阴影部分内的概率为