题目内容
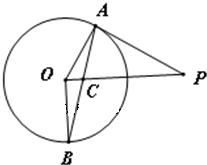 如图,已知PA与圆O相切于点A,OB⊥OP,AB交PO与点C.
如图,已知PA与圆O相切于点A,OB⊥OP,AB交PO与点C.(Ⅰ)求证:PA=PC;
(Ⅱ)若圆O的半径为3,|OP|=5,求BC的长.
考点:与圆有关的比例线段
专题:立体几何
分析:(1)由于PA与圆O相切于点A,可得OA⊥AP,于是∠OAC+∠PAC=90°.由于OB⊥OP,可得∠OCB+∠B=90°.利用OA=OB,可得∠OAC=∠OBC.可得∠PAC=∠OCB.利用对顶角相等可得∠OCB=∠PCA,进而得到∠PAC=∠PCA,即可证明PA=PC.
(2)在Rt△OAP中,利用勾股定理可得AP=
=
,即可得出PC=4.进而得到OC=OP-CP.在Rt△OBC中,利用勾股定理可得BC2=OB2+OC2即可.
(2)在Rt△OAP中,利用勾股定理可得AP=
| OP2-OA2 |
| 52-32 |
解答:
(1)证明:∵PA与圆O相切于点A,
∴OA⊥AP,∴∠OAC+∠PAC=90°.
∵OB⊥OP,∴∠OCB+∠B=90°.
∵OA=OB,∴∠OAC=∠OBC.
∴∠PAC=∠OCB,
又∵∠OCB=∠PCA,
∴∠PAC=∠PCA,
∴PA=PC.
(2)解:在Rt△OAP中,AP=
=
=4.
∴PC=4.
∴OC=OP-CP=1.
在Rt△OBC中,BC2=OB2+OC2=32+12=10.
∴BC=
.
∴OA⊥AP,∴∠OAC+∠PAC=90°.
∵OB⊥OP,∴∠OCB+∠B=90°.
∵OA=OB,∴∠OAC=∠OBC.
∴∠PAC=∠OCB,
又∵∠OCB=∠PCA,
∴∠PAC=∠PCA,
∴PA=PC.
(2)解:在Rt△OAP中,AP=
| OP2-OA2 |
| 52-32 |
∴PC=4.
∴OC=OP-CP=1.
在Rt△OBC中,BC2=OB2+OC2=32+12=10.
∴BC=
| 10 |
点评:本题考查了圆的切线的性质、勾股定理、圆的性质、对顶角相等的性质、等角对等边的性质等基础知识,属于基础题.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
函数f(x)=2x2-kx-8在区间[1,2]上不单调,则实数k的取值范围为( )
| A、[4,8] |
| B、(-∞,4]∪[8,+∞) |
| C、(-∞,4)∪(8,+∞) |
| D、(4,8) |
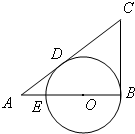 如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则AB的长为
如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则AB的长为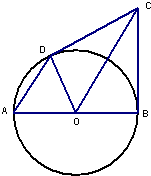 (几何证明选讲选做题)如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD,若OB=3,OC=5,则CD=
(几何证明选讲选做题)如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD,若OB=3,OC=5,则CD= 已知函数f(x)=lg(2+x)+lg(2-x).
已知函数f(x)=lg(2+x)+lg(2-x).