题目内容
对于定义域为[0,1]的函数f(x),如果同时满足以下三个条件:
①对任意的x∈[0,1],总有f(x)≥0
②f(1)=1
③若x1≥0,x2≥0,x1+x2≤1,都有f(x1+x2)≥f(x1)+f(x2) 成立;则称函数f(x)为?函数.下面有三个命题:
(1)若函数f(x)为?函数,则f(0)=0;
(2)函数f(x)=2x-1(x∈[0,1])是?函数;
(3)若函数f(x)是?函数,假定存在x0∈[0,1],使得f(x0)∈[0,1],且f[f(x0)]=x0,则f(x0)=x0;
其中真命题是 .(填上所有真命题的序号)
①对任意的x∈[0,1],总有f(x)≥0
②f(1)=1
③若x1≥0,x2≥0,x1+x2≤1,都有f(x1+x2)≥f(x1)+f(x2) 成立;则称函数f(x)为?函数.下面有三个命题:
(1)若函数f(x)为?函数,则f(0)=0;
(2)函数f(x)=2x-1(x∈[0,1])是?函数;
(3)若函数f(x)是?函数,假定存在x0∈[0,1],使得f(x0)∈[0,1],且f[f(x0)]=x0,则f(x0)=x0;
其中真命题是
考点:命题的真假判断与应用
专题:综合题,函数的性质及应用
分析:(1)依题意,令x1=x2=0可得f(0)≥f(0)+f(0)⇒f(0)≤0,对任意的x∈[0,1],总有f(x)≥0,由此可证f(0)=0;
(2)f(x)=2x-1在[0,1]满足条件①f(x)≥0,也满足条件②f(1)=1.若x1≥0,x2≥0,x1+x2≤1,满足条件③,从而得证f(x)是?函数;
(3)由条件③知,任给m、n∈[0,1],当m<n时,由m<n知n-m∈[0,1],f(n)=f(n-m+m)≥f(n-m)+f(m)≥f(m).由此能够推导出f(x0)=x0.
(2)f(x)=2x-1在[0,1]满足条件①f(x)≥0,也满足条件②f(1)=1.若x1≥0,x2≥0,x1+x2≤1,满足条件③,从而得证f(x)是?函数;
(3)由条件③知,任给m、n∈[0,1],当m<n时,由m<n知n-m∈[0,1],f(n)=f(n-m+m)≥f(n-m)+f(m)≥f(m).由此能够推导出f(x0)=x0.
解答:
解:(1)∵对任意的x∈[0,1],总有f(x)≥0,
又x1≥0,x2≥0,x1+x2≤1,都有f(x1+x2)≥f(x1)+f(x2) 成立,
∴取x1=x2=0得:f(0)≥f(0)+f(0),即f(0)≤0,
∴f(0)=0,即(1)正确;
(2)显然f(x)=2x-1在[0,1]满足条件①f(x)≥0;
也满足条件②f(1)=1.
若x1≥0,x2≥0,x1+x2≤1,
则f(x1+x2)-[f(x1)+f(x2)]
=2x1+x2-1-[(2x1-1)+(2x2-1)]
=2x1+x2-2x1-2x2+1
=(2x2-1)(2x1-1)≥0,即满足条件③,
故g(x)是?函数,即(2)正确;
(3)由条件③知,任给m、n∈[0,1],当m<n时,由m<n知n-m∈[0,1],
∴f(n)=f(n-m+m)≥f(n-m)+f(m)≥f(m).
若x0<f(x0),则f(x0)≤f[f(x0)]=x0,前后矛盾;
若x0>f(x0),则f(x0)≥f[f(x0)]=x0,前后矛盾.
故f(x0)=x0,即(3)正确;
故答案为:(1)(2)(3).
又x1≥0,x2≥0,x1+x2≤1,都有f(x1+x2)≥f(x1)+f(x2) 成立,
∴取x1=x2=0得:f(0)≥f(0)+f(0),即f(0)≤0,
∴f(0)=0,即(1)正确;
(2)显然f(x)=2x-1在[0,1]满足条件①f(x)≥0;
也满足条件②f(1)=1.
若x1≥0,x2≥0,x1+x2≤1,
则f(x1+x2)-[f(x1)+f(x2)]
=2x1+x2-1-[(2x1-1)+(2x2-1)]
=2x1+x2-2x1-2x2+1
=(2x2-1)(2x1-1)≥0,即满足条件③,
故g(x)是?函数,即(2)正确;
(3)由条件③知,任给m、n∈[0,1],当m<n时,由m<n知n-m∈[0,1],
∴f(n)=f(n-m+m)≥f(n-m)+f(m)≥f(m).
若x0<f(x0),则f(x0)≤f[f(x0)]=x0,前后矛盾;
若x0>f(x0),则f(x0)≥f[f(x0)]=x0,前后矛盾.
故f(x0)=x0,即(3)正确;
故答案为:(1)(2)(3).
点评:本题考查命题的真假判断与应用,着重考查函数值的求法,解题时要认真审题,细心挖掘题设中的隐含条件,考查等价转化思想与抽象思维、逻辑思维能力,属于难题.

练习册系列答案
相关题目
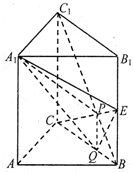 如图在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1=2,E是BB1的中点,且CE交BC1于点P,点Q在线段BC上,CQ=2QB.
如图在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1=2,E是BB1的中点,且CE交BC1于点P,点Q在线段BC上,CQ=2QB.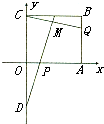 如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,|OC|=
如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,|OC|=