题目内容

已知sinα=
5
13
，且α∈（
π
2
，π）．
（1）求tanα的值；
（2）求
cos2α
2
sin(α+
π
4
)
的值．
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：（1）由sinα的值及α的范围，利用同角三角函数间基本关系求出cosα的值，即可确定出tanα的值；
（2）原式分子利用二倍角的余弦函数公式化简，分母利用两角和与差的正弦函数公式化简，约分后将各自的值代入计算即可求出值．
解答： 解：（1）∵sinα=
5
13
，且α∈（
π
2
，π），
∴cosα=-
1-sin2α
=-
12
13
，
则tanα=
sinα
cosα
=-
5
12
；
（2）∵sinα=
5
13
，cosα=-
12
13
，
∴原式=
cos2α-sin2α
2
(
2
2
sinα+
2
2
cosα)
=
(cosα+sinα)(cosα-sinα)
cosα+sinα
=cosα-sinα=-
12
13
-
5
13
=-
17
13
．
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
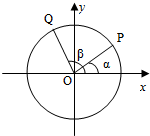如图，以Ox为始边分别作角α与β（0＜α＜β＜π），它们的终边分别与单位圆相交于点P、Q，已知点P的坐标为（
3
5
，
4
5
）．
（1）求sin2α的值；
（2）若β-α=
π
2
，求cos（α+β）的值．
点P是椭圆
x2
25
+
y2
16
=1上的一点，F1、F2是椭圆的两个焦点，且∠F1PF2=60°，求△F1PF2的面积．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
6
3
，短轴一个端点到右焦点的距离为
3
，试求椭圆C的标准方程．
如图所示茎叶图记录了甲，乙两组各三名同学在期末考试中的数学成绩（满分为100分）．乙组记录中有一个数字模糊，无法确认，假设这个数字具有随机性，并在图中以a表示．
（Ⅰ）若甲，乙两个小组的数学平均成绩相同，求a的值．
（Ⅱ）求乙组平均成绩超过甲组平均成绩的概率．
（Ⅲ）当a=2时，分别从甲，乙两组同学中各随机选取一名同学，求这两名同学的数学成绩之差的绝对值为2分的概率．
设二次函数f（x）=-x2+2x．
（Ⅰ）求函数y=（
1
2
）f（x）的最小值；
（Ⅱ）问是否存在这样的正数m，n，当x∈[m，n]时，g（x）=f（x），且g（x）的值域为[
1
n
，
1
m
]？若存在，求出所有的m，n的值，若不存在，请说明理由．
已知：函数f（x）=
1
2
（sinx+|sinx|），x∈R
（1）求函数f（x）的周期T，与单调增区间．
（2）函数y=f（x）与y=lgx的图象有几个公共交点．
（3）设关于x的函数g（x）=-2sin2x-2acosx-2a+1的最小值为h（a），试确定满足h（a）=
1
2
的a的值，并对此时的a值求g（x）的最小值．
不等式x（x-2）＜0的解集是
 
．
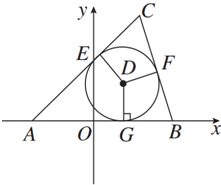△ABC的顶点A（-5，0），B（5，0），△ABC的内切圆圆心在直线x=3上，则顶点C的轨迹方程是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网