题目内容
11．
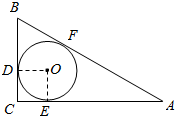如图，在Rt△ABC中，∠C=90°，BC=a，AC=b，AB=c，⊙O为ABC的内切圆，D，E，F分别为切点，O的半径为r，试用含a，b，c的代数式表示r．
分析 根据切线长定理，找出a，b，c，r的关系，可得答案．
解答 解：在Rt△ABC中，∠C=90°，BC=a，AC=b，AB=c，⊙O为ABC的内切圆，D，E，F分别为切点，O的半径为r，
则BD=BF，CD=CE=r，AE=AF，
a=BD+CD=BD+r，
b=AE+CE=AE+r，
c=AF+BF，
a+b-c=2r，
∴r=$\frac{1}{2}$（a+b-c）
点评 本题考查的知识点是切线长定理，本题的结论是计算三角形内切圆半径的重要途径，建议牢记．
练习册系列答案
相关题目
1．某几何体的三视图如图所示，则该几何体的体积是（ ）
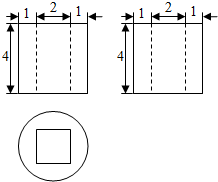
| A． | 16π-16 | B． | 16π | C． | 16π-8 | D． | 64 |
6．方程lgx+x=0的根所在的区间是（ ）
| A． | $（0，\frac{1}{4}）$ | B． | $（\frac{1}{4}，\frac{1}{2}）$ | C． | $（\frac{1}{2}，\frac{3}{4}）$ | D． | $（\frac{3}{4}，1）$ |
如图，在直三棱柱ABC-A1B1C1中，CC1=AC=2，AB=BC，D是BC1上的点．且CD⊥平面ABC1．
1．设a、b是两条不同的直线，α、β是两个不同的平面，下列命题中正确的是（ ）
| A． | 若α⊥β，a?α，b?β，则a⊥b | B． | 若α∥β，a?α，b?β，则a∥b | ||
| C． | 若α⊥β，a?α，a⊥b，则b∥β | D． | 若a⊥α，a∥b，b∥β，则α⊥β |