题目内容
2.若双曲线的渐近线方程为2x±y=0,且过点(1,2$\sqrt{2}$),则双曲线的方程为$\frac{{y}^{2}}{4}-{x}^{2}=1$.分析 分两种情况使用待定系数法求出.
解答 解:(1)若双曲线焦点在x轴上,设双曲线方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$,
∴$\left\{\begin{array}{l}{\frac{b}{a}=2}\\{\frac{1}{{a}^{2}}-\frac{8}{{b}^{2}}=1}\end{array}\right.$,方程组无解.
(2)若双曲线焦点在y轴上,设双曲线方程为$\frac{{y}^{2}}{{a}^{2}}-\frac{{x}^{2}}{{b}^{2}}=1$,
∴$\left\{\begin{array}{l}{\frac{a}{b}=2}\\{\frac{8}{{a}^{2}}-\frac{1}{{b}^{2}}=1}\end{array}\right.$,解得a=2,b=1.
∴双曲线方程为$\frac{{y}^{2}}{4}-{x}^{2}=1$.
故答案为$\frac{{y}^{2}}{4}-{x}^{2}=1$.
点评 本题考查了双曲线的方程与性质,常采用待定系数法求方程.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
12.已知F是抛物线y2=4x的焦点,点A,B在该抛物线上且位于x轴的两侧,OA⊥OB(其中O为坐标原点),则△AOB与△AOF面积之和的最小值是( )
| A. | 16 | B. | 8$\sqrt{3}$ | C. | 8$\sqrt{5}$ | D. | 18 |
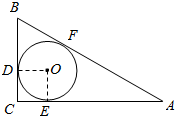 如图,在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c,⊙O为ABC的内切圆,D,E,F分别为切点,O的半径为r,试用含a,b,c的代数式表示r.
如图,在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c,⊙O为ABC的内切圆,D,E,F分别为切点,O的半径为r,试用含a,b,c的代数式表示r.