题目内容
 如图所示,将正整数排成三角形数阵,每排的数称为一个群,从上到下顺次为第一群,第二群,…,第n群,…,第n群恰好n个数,则第n群中n个数的和是
如图所示,将正整数排成三角形数阵,每排的数称为一个群,从上到下顺次为第一群,第二群,…,第n群,…,第n群恰好n个数,则第n群中n个数的和是考点:归纳推理
专题:规律型,等差数列与等比数列
分析:观察图例,我们可以得到每一行的数第一个构成一个以1为首项,以2为公比的等比数列,每一行的从右边的第k个数都构成一个以2k为公差的等差数列,进而可分析出第n群中n个数的和的表达式.
解答:
解:观察图例,我们可以得到每一行的数第一个构成一个以1为首项,以2为公比的等比数列,
每一行的从右边的第k个数都构成一个以2k为公差的等差数列,
故第n群的第一个数为:2n-1,
第n群的第二个数为:2n-2+2n-1=3•2n-2,
第n群的第三个数为:2n-3+2×2n-2=5•2n-3,
…
第n群的第n-1个数为:2+(n-2)×22=(2n-3)•2,
第n群的第n个数为:1+(n-1)×2=2n-1,
故第n群中n个数的和Sn=2n-1+3•2n-2+5•2n-3+…+(2n-3)•2+(2n-1),…①
故2Sn=2n+3•2n-1+5•2n-2+…+(2n-3)•22+(2n-1)•2,…②
②-①得:
Sn=2n+2(2n-1+2n-2+…+22+2)-(2n-1)=3•2n-2n-3,
故答案为:3•2n-2n-3
每一行的从右边的第k个数都构成一个以2k为公差的等差数列,
故第n群的第一个数为:2n-1,
第n群的第二个数为:2n-2+2n-1=3•2n-2,
第n群的第三个数为:2n-3+2×2n-2=5•2n-3,
…
第n群的第n-1个数为:2+(n-2)×22=(2n-3)•2,
第n群的第n个数为:1+(n-1)×2=2n-1,
故第n群中n个数的和Sn=2n-1+3•2n-2+5•2n-3+…+(2n-3)•2+(2n-1),…①
故2Sn=2n+3•2n-1+5•2n-2+…+(2n-3)•22+(2n-1)•2,…②
②-①得:
Sn=2n+2(2n-1+2n-2+…+22+2)-(2n-1)=3•2n-2n-3,
故答案为:3•2n-2n-3
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
把函数f(x)=sin(2x-
)的图象向左平移φ(0<φ<π)个单位可以得到函数g(x)的图象,若g(x)的图象关于y轴对称,则φ的值为( )
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
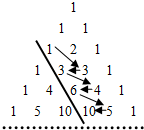 如图,在杨辉三角中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S27的值为
如图,在杨辉三角中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S27的值为 一个街区有南北走向6条街和东西走向5条街,某人从街道的西北角A点走到东南角B点,最短的走法有
一个街区有南北走向6条街和东西走向5条街,某人从街道的西北角A点走到东南角B点,最短的走法有