题目内容
12.在?ABCD中,AB=AC=1,∠ACD=90°,将它沿着对角线AC折起,使AB与CD成60°角,则BD的长度为( )| A. | 2 | B. | 2或$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 3$\sqrt{2}$或2$\sqrt{2}$ |
分析 利用向量的加法,$\overrightarrow{BD}$=$\overrightarrow{BA}$+$\overrightarrow{AC}$+$\overrightarrow{CD}$,等式两边进行平方,求出BD的长度即可.
解答 解:∵∠ACD=90°,∴$\overrightarrow{AC}$$•\overrightarrow{CD}$=0.
同理$\overrightarrow{BA}$$•\overrightarrow{AC}$=0.
∵AB和CD成60°角,∴<$\overrightarrow{BA}$,$\overrightarrow{CD}$>=60°或120°.
∵$\overrightarrow{BD}$=$\overrightarrow{BA}$+$\overrightarrow{AC}$+$\overrightarrow{CD}$,
∴${\overrightarrow{BD}}^{2}$=3+2×1×1×cos<$\overrightarrow{BA}$,$\overrightarrow{CD}$>
∴|$\overrightarrow{BD}$|=2或$\sqrt{2}$,
故选B.
点评 本小题主要考查异面直线所成的角,以及数量积表示两个向量的夹角,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
相关题目
10.如图的三视图所对应的立体图形可以是( )
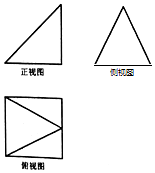

| A. | 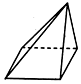 | B. | 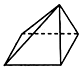 | C. | 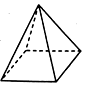 | D. |  |
3.已知数列{an}的首项为a1=1,且满足an+1=$\frac{1}{2}$an+$\frac{1}{{2}^{n}}$,则此数列的第4项是( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{8}$ |
 如图,在三棱锥S-ABC中,AS=AB,CS=CB,点E,F,G分别是棱SA,SB,SC的中点.求证:
如图,在三棱锥S-ABC中,AS=AB,CS=CB,点E,F,G分别是棱SA,SB,SC的中点.求证: