题目内容
1．已知正四棱台的上、下底面面积分别为4、16，一侧面面积为12，分别求该棱台的斜高、高、侧棱长．分析 取上底A1B1C1D1的中心O1和下底ABCD的中心O，连结OO1，过O1作O1F⊥A1B1，交A1B1于F，过O作OE⊥AB，交AB于E，过F作FN⊥OE，交OE于N，由此能求出正四棱台的斜高、高、侧棱长．
解答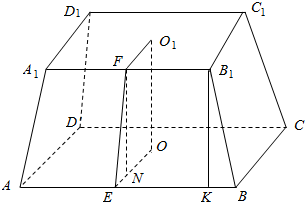 
解：取上底A1B1C1D1的中心O1和下底ABCD的中心O，连结OO1，
过O1作O1F⊥A1B1，交A1B1于F，过O作OE⊥AB，交AB于E，
过F作FN⊥OE，交OE于N，
由题意，正四棱台的上、下底面边长分别为2，4，
$\frac{2+4}{2}×EF$=12，∴正四棱台的斜高EF=4，
则正四棱台的高OO1=FN=$\sqrt{16-（2-1）^{2}}$=$\sqrt{15}$．
侧棱长=$\sqrt{16+1}$=$\sqrt{17}$
点评 本题考查正四棱台的高和斜高的求法，是基础题，解题时要认真审题，注意空间思维能力和下四棱台的结构特征的合理运用．
练习册系列答案
备战中考寒假系列答案
相关题目
12．在?ABCD中，AB=AC=1，∠ACD=90°，将它沿着对角线AC折起，使AB与CD成60°角，则BD的长度为（ ）
| A． | 2 | B． | 2或$\sqrt{2}$ | C． | $\sqrt{2}$ | D． | 3$\sqrt{2}$或2$\sqrt{2}$ |
16．在等差数列{an}中，a1=-2 012，其前n项和为Sn，若$\frac{{{S_{12}}}}{12}-\frac{{{S_{10}}}}{10}$=2，则S2012的值等于（ ）
| A． | -2 011 | B． | -2 012 | C． | -2 010 | D． | -2 013 |
6．下列不等式中，正确的是（ ）
| A． | 若x∈R，则$x+\frac{4}{x}≥4$ | B． | 若x∈R，则${x^2}+2+\frac{1}{{{x^2}+2}}≥2$ | ||
| C． | 若x∈R，则${x^2}+1+\frac{1}{{{x^2}+1}}≥2$ | D． | 若a、b为正实数，则$\frac{{\sqrt{a}+\sqrt{b}}}{2}≥\sqrt{ab}$ |
13．已知函数y=f（n），满足f（0）=3，且f （n）=nf（n-1），n∈N+，则f（3）=（ ）
| A． | 6 | B． | 9 | C． | 18 | D． | 24 |
11．已知i为虚数单位，则复数$\frac{1+i}{i}$=（ ）
| A． | 1+i | B． | 1-i | C． | 1+$\frac{i}{2}$ | D． | 1-$\frac{i}{2}$ |