题目内容
2. 如图,在三棱锥S-ABC中,AS=AB,CS=CB,点E,F,G分别是棱SA,SB,SC的中点.求证:
如图,在三棱锥S-ABC中,AS=AB,CS=CB,点E,F,G分别是棱SA,SB,SC的中点.求证:(1)平面EFG∥平面ABC;
(2)SB⊥AC.
分析 (1)证明EF∥平面ABC,EG∥平面ABC,即可证明平面EFG∥平面ABC;
(2)连接AF,CF,转化证明SB⊥平面AFC,即可得证SB⊥AC.
解答 证明:(1)∵E、G分别为SA、SC的中点,
∴EF、EG分别是△SAB、△SAC的中位线,可得EF∥AB且EG∥AC.
∵EF?平面ABC,AB?平面ABC,
∴EF∥平面ABC,同理可得EG∥平面ABC
又∵EF、EG是平面EFG内的相交直线,
∴平面EFG∥平面ABC;
(2)连接AF,CF,
∵AS=AB,CS=CB,
∴SB⊥AF,SB⊥FC,
∵AF∩CF=F,
∴SB⊥平面AFC,
∵AC?平面AFC,
∴SB⊥AC.
点评 本题考查了线面、面面平行的判定,考查空间直线的垂直的判断,运用直线与平面的垂直转化证明,属于中档题,掌握好基本定理即可.

练习册系列答案
相关题目
12.在?ABCD中,AB=AC=1,∠ACD=90°,将它沿着对角线AC折起,使AB与CD成60°角,则BD的长度为( )
| A. | 2 | B. | 2或$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 3$\sqrt{2}$或2$\sqrt{2}$ |
13.已知函数y=f(n),满足f(0)=3,且f (n)=nf(n-1),n∈N+,则f(3)=( )
| A. | 6 | B. | 9 | C. | 18 | D. | 24 |
11.已知i为虚数单位,则复数$\frac{1+i}{i}$=( )
| A. | 1+i | B. | 1-i | C. | 1+$\frac{i}{2}$ | D. | 1-$\frac{i}{2}$ |

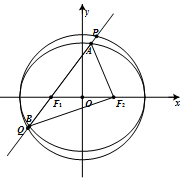 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)和圆O:x2+y2=a2,F1(-1,0),F2(1,0)分别是椭圆的左、右两焦点,过F1且倾斜角为α$({α∈({0,\frac{π}{2}}]})$的动直线l交椭圆C于A,B两点,交圆O于P,Q两点(如图所示,点A在x轴上方).当α=$\frac{π}{4}$时,弦PQ的长为$\sqrt{14}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)和圆O:x2+y2=a2,F1(-1,0),F2(1,0)分别是椭圆的左、右两焦点,过F1且倾斜角为α$({α∈({0,\frac{π}{2}}]})$的动直线l交椭圆C于A,B两点,交圆O于P,Q两点(如图所示,点A在x轴上方).当α=$\frac{π}{4}$时,弦PQ的长为$\sqrt{14}$. 