题目内容
7．若直线y=kx+3与直线y=$\frac{1}{k}$x-5的交点在第一象限，则k的取值范围是0＜k＜1．分析 根据第一象限点的特点，得到关于k的不等式组解之．
解答 解：联立直线y=kx+3与直线y=$\frac{1}{k}$x-5，得到交点坐标为（$\frac{8k}{1-{k}^{2}}$，$\frac{5{k}^{2}+3}{1-{k}^{2}}$），
因为y=kx+3与直线y=$\frac{1}{k}$x-5的交点在第一象限，
得$\frac{8k}{1-{k}^{2}}$＞0且$\frac{5{k}^{2}+3}{1-{k}^{2}}$＞0，解得0＜k＜1，
故答案为：0＜k＜1．
点评 本题考查学生会利用两直线方程联立得到方程组求出交点坐标，掌握第一象限点坐标的特点，会求不等式组的解集．
练习册系列答案
相关题目
15．设随机变量ξ等可能取值1，2，3，4，…，n，如果p（ξ＜4）=0.3，则n的值为（ ）
| A． | 3 | B． | 4 | C． | 10 | D． | 不能确定 |
12．在?ABCD中，AB=AC=1，∠ACD=90°，将它沿着对角线AC折起，使AB与CD成60°角，则BD的长度为（ ）
| A． | 2 | B． | 2或$\sqrt{2}$ | C． | $\sqrt{2}$ | D． | 3$\sqrt{2}$或2$\sqrt{2}$ |
19．若曲线C1：y=x2与曲线C2：y=aex（a＞0）至少存在两个交点，则a的取值范围为（ ）
| A． | [$\frac{8}{{e}^{2}}$，+∞） | B． | （0，$\frac{8}{{e}^{2}}$] | C． | [$\frac{4}{{e}^{2}}$，+∞） | D． | （0，$\frac{4}{{e}^{2}}$] |
16．在等差数列{an}中，a1=-2 012，其前n项和为Sn，若$\frac{{{S_{12}}}}{12}-\frac{{{S_{10}}}}{10}$=2，则S2012的值等于（ ）
| A． | -2 011 | B． | -2 012 | C． | -2 010 | D． | -2 013 |
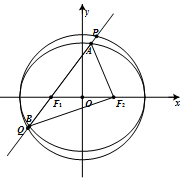已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）和圆O：x2+y2=a2，F1（-1，0），F2（1，0）分别是椭圆的左、右两焦点，过F1且倾斜角为α$（{α∈（{0，\frac{π}{2}}]}）$的动直线l交椭圆C于A，B两点，交圆O于P，Q两点（如图所示，点A在x轴上方）．当α=$\frac{π}{4}$时，弦PQ的长为$\sqrt{14}$．