题目内容
9.设全集U={x∈R|x>0},函数f(x)=$\sqrt{1-lnx}$的定义域为A,则∁UA为( )| A. | (e,+∞) | B. | [e,+∞) | C. | (0,e) | D. | (0,e] |
分析 求出集合A,再根据补集的定义写出∁UA.
解答 解:全集U={x∈R|x>0},
函数f(x)=$\sqrt{1-lnx}$的定义域为
A={x|1-lnx≥0}={x|0<x≤e},
∴∁UA={x|x>e}=(e,+∞).
故选:A.
点评 本题考查了集合的化简与运算问题,是基础题目.

练习册系列答案
相关题目
4.下列说法正确的是( )
| A. | 以直角三角形一边为轴旋转所得的旋转体是圆锥 | |
| B. | 用一个平面去截圆锥,得到一个圆锥和一个圆台 | |
| C. | 正棱锥的棱长都相等 | |
| D. | 棱柱的侧棱都相等,侧面是平行四边形 |
1.对任意实数a,b定义运算“⊙”:a⊙b=$\left\{\begin{array}{l}a,a-b≤1\\ b,a-b>1\end{array}$设f(x)=2x+1⊙(1-x),若函数f(x)与函数g(x)=x2-6x在区间(m,m+1)上均为减函数,且m∈{-1,0,1,3},则m的值为( )
| A. | 0 | B. | -1或0 | C. | 0或1 | D. | 0或1或3 |
4.要得到函数y=cos2x-sin2x的图象,只需将函数y=sin2x的图象( )
| A. | 向左平移$\frac{π}{2}$个单位长度 | B. | 向右平移$\frac{π}{2}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向右平移$\frac{π}{4}$个单位长度 |
1.从区间[-2,9]中任取一个实数a,则恰使得函数f(x)=ln(ax2-2x+a)存在最大值或最小值的概率为( )
| A. | $\frac{1}{11}$ | B. | $\frac{8}{11}$ | C. | $\frac{9}{11}$ | D. | $\frac{10}{11}$ |
19.设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的半焦距为c,(a,0)、(0,b)为直线l上两点,已知原点到直线l的距离为$\frac{{\sqrt{3}}}{4}$c,则双曲线的离心率为( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{3}$或2 | C. | 2 | D. | 2或 $\frac{{2\sqrt{3}}}{3}$ |
 如图,已知焦点在y轴上的椭圆E的中心是原点O,离心率为$\frac{{\sqrt{3}}}{2}$,以椭圆E的短轴的两端点和两焦点所围成的四边形的周长为8,直线l:y=kx+m与y轴交于点M,与椭圆E交于不同两点A,B.
如图,已知焦点在y轴上的椭圆E的中心是原点O,离心率为$\frac{{\sqrt{3}}}{2}$,以椭圆E的短轴的两端点和两焦点所围成的四边形的周长为8,直线l:y=kx+m与y轴交于点M,与椭圆E交于不同两点A,B.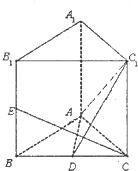 如图在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=2$\sqrt{2}$,BC=BB1=4,D、E分别为BC,BB1的中点.
如图在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=2$\sqrt{2}$,BC=BB1=4,D、E分别为BC,BB1的中点.