题目内容
4.已知某正方体的外接球的表面积是16π,则这个正方体的棱长是( )| A. | $\frac{{2\sqrt{2}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{4\sqrt{2}}}{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
分析 根据正方体外接球的表面积求出棱长即可.
解答 解:设正方体的棱长为a,则正方体的体对角线的长就是外接球的直径,
∴外接球的半径为:$\frac{\sqrt{3}}{2}$a,
∵正方体外接球表面积是16π,
∴4π($\frac{\sqrt{3}}{2}$a)2=16π,
解得a=$\frac{4\sqrt{3}}{3}$.
故选:D.
点评 此题考查了点、线、面间的距离计算,熟练掌握正方体外接球表面积公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.对标有不同编号的形状大小完全一样的5件正品和3件次品进行检测,现不放回地依次取出2件,则在第一次取出正品的条件下,第二次也取出正品的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{14}$ | D. | $\frac{4}{7}$ |
19.设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的半焦距为c,(a,0)、(0,b)为直线l上两点,已知原点到直线l的距离为$\frac{{\sqrt{3}}}{4}$c,则双曲线的离心率为( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{3}$或2 | C. | 2 | D. | 2或 $\frac{{2\sqrt{3}}}{3}$ |
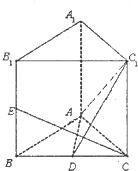 如图在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=2$\sqrt{2}$,BC=BB1=4,D、E分别为BC,BB1的中点.
如图在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=2$\sqrt{2}$,BC=BB1=4,D、E分别为BC,BB1的中点. 如图,在三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.
如图,在三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.