题目内容
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为H.则以下命题中,错误的命题是( )
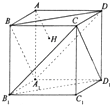

| A、点H是△A1BD的垂心 |
| B、AH垂直平面CB1D1 |
| C、直线AH和BB1所成角为45° |
| D、AH的延长线经过点C1 |
考点:命题的真假判断与应用,异面直线及其所成的角,直线与平面垂直的判定
专题:简易逻辑
分析:首先,判断三棱锥 A-BA1D为正三棱锥,然后,得到△BA1D为正三角形,得到H为A在平面A1BD内的射影,然后,根据平面A1BD与平面B1CD1平行,得到选项B正确,最后,结合线面角和对称性求解.
解答:
解:∵AB=AA1=AD,
BA1=BD=A1D,
∴三棱锥 A-BA1D为正三棱锥,
∴点H是△A1BD的垂心;
故选项A正确;
对于选项B:
∵平面A1BD与平面B1CD1平行,
∵AH⊥平面A1BD,
∵平面A1BD⊥平面BC1D,
∴AH垂直平面CB1D1,
选项B正确;
根据正方体的对称性得到
AH的延长线经过C1,
∴选项D正确;
对于选项C,
∵AA1∥BB1,
∴∠A1AH就是直线AH和BB1所成角,
在直角三角形AHA1中,
∵AA1=1,A1H=
×
×
=
,
∴sin∠A1AH=
,
所以选项C错误,
故选C.
BA1=BD=A1D,
∴三棱锥 A-BA1D为正三棱锥,
∴点H是△A1BD的垂心;
故选项A正确;
对于选项B:
∵平面A1BD与平面B1CD1平行,
∵AH⊥平面A1BD,
∵平面A1BD⊥平面BC1D,
∴AH垂直平面CB1D1,
选项B正确;
根据正方体的对称性得到
AH的延长线经过C1,
∴选项D正确;
对于选项C,
∵AA1∥BB1,
∴∠A1AH就是直线AH和BB1所成角,
在直角三角形AHA1中,
∵AA1=1,A1H=
| 2 |
| 3 |
| ||
| 2 |
| 2 |
| ||
| 3 |
∴sin∠A1AH=
| ||
| 3 |
所以选项C错误,
故选C.
点评:本题重点考查空间中点线面的位置关系,属于中档题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
任取三个整数,至少有一个数为偶数的概率为( )
| A、0.125 | B、0.25 |
| C、0.5 | D、0.875 |
下列命题中的真命题是( )
| A、2+4=7 |
| B、若x=1,则x2-1=0 |
| C、若x2=1,则x=1 |
| D、3能被2整除 |
已知直线(m+2)x+(m+1)y+1=0上存在点(x,y)满足
,则m的取值范围为( )
|
A、[-
| ||||
B、(-∞,-
| ||||
C、[-1,
| ||||
D、[-
|