题目内容
已知函数f(x)=ax+blnx+c(a,b,c是常数)在x=e处的切线方程为(e-1)x+ey-e=0,且f(1)=0.
(Ⅰ)求常数a,b,c的值;
(Ⅱ)若函数g(x)=x2+mf(x)(m∈R)在区间(1,3)内不是单调函数,求实数m的取值范围.
(Ⅰ)求常数a,b,c的值;
(Ⅱ)若函数g(x)=x2+mf(x)(m∈R)在区间(1,3)内不是单调函数,求实数m的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(Ⅰ)利用f(x)在x=e处的切线方程,可得f′(e)=-
,且f(e)=2-e,f(1)=a+c=0,即可求常数a,b,c的值;
(Ⅱ)求导函数,令d(x)=2x2-mx+m(x>0),分类讨论,建立不等式,即可求实数m的取值范围.
| e-1 |
| e |
(Ⅱ)求导函数,令d(x)=2x2-mx+m(x>0),分类讨论,建立不等式,即可求实数m的取值范围.
解答:
解:(Ⅰ)由题设知,f(x)的定义域为(0,+∞),f′(x)=a+
,
∵f(x)在x=e处的切线方程为(e-1)x+ey-e=0,
∴f′(e)=-
,且f(e)=2-e,即a+
=-
,且ae+b+c=2-e,
又f(1)=a+c=0,解得a=-1,b=1,c=1…(5分)
(Ⅱ)由(Ⅰ)知f(x)=-x+lnx+1(x>0)
∴g(x)=x2+mf(x)=x2-mx+mlnx+m(x>0)
∴g′(x)=2x-m+
=
(2x2-mx+m)(x>0)…(7分)
令d(x)=2x2-mx+m(x>0).
(ⅰ)当函数g(x)在(1,3)内有一个极值时,g′(x)=0在(1,3)内有且仅有一个根,
即d(x)=2x2-mx+m=0在(1,3)内有且仅有一个根,
又∵d(1)=2>0,当d(3)=0,即m=9时,d(x)=2x2-mx+m=0在(1,3)内有且仅有一个根x=
,当d(3)≠0时,应有d(3)<0,即2×32-3m+m<0,解得m>9,
∴m≥9.
(ⅱ)当函数g(x)在(1,3)内有两个极值时,g′(x)=0在(1,3)内有两个根,
即二次函数d(x)=2x2-mx+m=0在(1,3)内有两个不等根,
所以
,解得8<m<9.
综上,实数m的取值范围是(8,+∞)…(13分)
| b |
| x |
∵f(x)在x=e处的切线方程为(e-1)x+ey-e=0,
∴f′(e)=-
| e-1 |
| e |
| b |
| e |
| e-1 |
| e |
又f(1)=a+c=0,解得a=-1,b=1,c=1…(5分)
(Ⅱ)由(Ⅰ)知f(x)=-x+lnx+1(x>0)
∴g(x)=x2+mf(x)=x2-mx+mlnx+m(x>0)
∴g′(x)=2x-m+
| m |
| x |
| 1 |
| x |
令d(x)=2x2-mx+m(x>0).
(ⅰ)当函数g(x)在(1,3)内有一个极值时,g′(x)=0在(1,3)内有且仅有一个根,
即d(x)=2x2-mx+m=0在(1,3)内有且仅有一个根,
又∵d(1)=2>0,当d(3)=0,即m=9时,d(x)=2x2-mx+m=0在(1,3)内有且仅有一个根x=
| 3 |
| 2 |
∴m≥9.
(ⅱ)当函数g(x)在(1,3)内有两个极值时,g′(x)=0在(1,3)内有两个根,
即二次函数d(x)=2x2-mx+m=0在(1,3)内有两个不等根,
所以
|
综上,实数m的取值范围是(8,+∞)…(13分)
点评:本题考查导数知识的运用,考查函数的极值,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
下列说法中,正确的是( )
| A、数据 5,4,4,3,5,2 的众数是 4 |
| B、一组数据的标准差是这组数据的方差的平方 |
| C、数据 2,3,4,5 的标准差是数据 4,6,8,10 的标准差的一半 |
| D、频率分布直方图中各小长方形的面积等于相应各组的频数 |
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为H.则以下命题中,错误的命题是( )
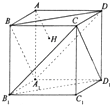

| A、点H是△A1BD的垂心 |
| B、AH垂直平面CB1D1 |
| C、直线AH和BB1所成角为45° |
| D、AH的延长线经过点C1 |
 如图,在四棱锥P-ABCD中,AB∥CD,△PAB和△PAD是两个边长为2的正三角形.DC=4,PD⊥PB,点E是CD的中点.
如图,在四棱锥P-ABCD中,AB∥CD,△PAB和△PAD是两个边长为2的正三角形.DC=4,PD⊥PB,点E是CD的中点.