题目内容
已知直线(m+2)x+(m+1)y+1=0上存在点(x,y)满足
,则m的取值范围为( )
|
A、[-
| ||||
B、(-∞,-
| ||||
C、[-1,
| ||||
D、[-
|
考点:简单线性规划
专题:不等式的解法及应用
分析:将直线进行整理,得到直线过定点(-1,1),作出不等式组对应的平面区域,根据条件得到A.B应该在直线l的两侧或在直线l上,即可得到结论.
解答:
解:∵直线l:(m+2)x+(m+1)y+1=0等价为m(x+y)+(2x+y+1)=0,
即
,解得
,
∴直线过定点P(-1,1),
作出不等式组对应的平面区域(阴影部分ABC),
要使直线(m+2)x+(m+1)y+1=0上存在点(x,y)满足
,
则必有点A(1,2),B(1,-1)在l的两侧或在l上.
得[(m+2)×1+(m+1)×2+1]•[(m+2)×1+(m+1)×(-1)+1]≤0,
即2(3m+5)≤0,
解得m≤-
.
故m的取值范围为(-∞,-
],
故选:B.
即
|
|
∴直线过定点P(-1,1),

作出不等式组对应的平面区域(阴影部分ABC),
要使直线(m+2)x+(m+1)y+1=0上存在点(x,y)满足
|
则必有点A(1,2),B(1,-1)在l的两侧或在l上.
得[(m+2)×1+(m+1)×2+1]•[(m+2)×1+(m+1)×(-1)+1]≤0,
即2(3m+5)≤0,
解得m≤-
| 5 |
| 3 |
故m的取值范围为(-∞,-
| 5 |
| 3 |
故选:B.
点评:本题主要考查线性规划的应用,根据条件求出直线过定点,以及利用不等式组作出平面区域是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
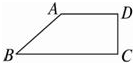 一个水平放置的平面图形的斜二测直观图是直角梯形(如图).∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为( )
一个水平放置的平面图形的斜二测直观图是直角梯形(如图).∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为( ) A、
| ||||||
B、2+
| ||||||
C、
| ||||||
D、
|
在锐角△ABC中,角A,B,C的对边分别为a,b,c.若ccosB+bcosC=2acosA,则角A为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为H.则以下命题中,错误的命题是( )
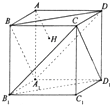

| A、点H是△A1BD的垂心 |
| B、AH垂直平面CB1D1 |
| C、直线AH和BB1所成角为45° |
| D、AH的延长线经过点C1 |