题目内容
已知Sn是等差数列{an}(n∈N*)的前n项和,且S6>S7>S5,有下列五个结论:
①d<0;
②S11>0;
③S12<0;
④数列{Sn}中的最大项为S11;
⑤数列{Sn}的前n项和Tn中最大为T12.
其中正确的个数是( )
①d<0;
②S11>0;
③S12<0;
④数列{Sn}中的最大项为S11;
⑤数列{Sn}的前n项和Tn中最大为T12.
其中正确的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:等差数列的性质
专题:综合题,等差数列与等比数列
分析:先由条件确定第六项和第七项的正负,进而确定公差的正负,再将S11,S12由第六项和第七项的正负判定.
解答:
解:∵等差数列{an}中,S6最大,且S6>S7>S5,
∴a1>0,d<0,①正确;
∵S6>S7>S5,
∴a6>0,a7<0,∴a1+6d<0,a1+5d>0,S6最大,
∴④⑤不正确;
S11=11a1+55d=11(a1+5d)>0,
S12=12a1+66d=12(a1+a12)=12(a6+a7)>0,
∴②正确,③错误
故选:B.
∴a1>0,d<0,①正确;
∵S6>S7>S5,
∴a6>0,a7<0,∴a1+6d<0,a1+5d>0,S6最大,
∴④⑤不正确;
S11=11a1+55d=11(a1+5d)>0,
S12=12a1+66d=12(a1+a12)=12(a6+a7)>0,
∴②正确,③错误
故选:B.
点评:本题考查等差数列的前n项和的最值.在等差数列中Sn存在最大值的条件是:a1>0,d<0.

练习册系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )


| A、45π | B、54π |
| C、72π | D、90π |
已知命题p:平行于同一直线的两个平面平行;命题q:垂直于同一平面的两条直线平行,那么( )
| A、“p或q”是假命题 |
| B、“p且q”是真命题 |
| C、“¬p或q”是假命题 |
| D、“¬p且q”是真命题 |
设n∈N*,曲线y=xn(1-x)在x=2处的切线与y轴交点的纵坐标为an,则a4为( )
| A、80 | B、32 |
| C、192 | D、256 |
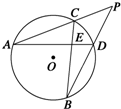 如图所示,⊙O的两条弦AD和CB相交于点E,AC和BD的延长线相交于点P,下面结论:
如图所示,⊙O的两条弦AD和CB相交于点E,AC和BD的延长线相交于点P,下面结论:①PA•PC=PD•PB;
②PC•CA=PB•BD;
③CE•CD=BE•BA;
④PA•CD=PD•AB.
其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知复数a+bi=
(a、b∈R),则z=b+(a-1)i在复平面上对应的点位于( )
| 2+i |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知角α的终边在函数y=2x(x>0)的图象上,则1-2sinαcosα-3cos2α的值( )
A、-
| ||
B、±
| ||
| C、-2 | ||
| D、±2 |