题目内容
7.如图,在棱长均相等的正三棱柱ABC-A1B1C1中,异面直线AA1与BC1的夹角为( )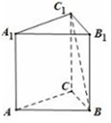
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 由AA1∥BB1,知∠B1BC1是异面直线AA1与BC1的夹角,由此能求出结果.
解答 解:在棱长均相等的正三棱柱ABC-A1B1C1中,
∵AA1∥BB1,
∴∠B1BC1是异面直线AA1与BC1的夹角,
∵在棱长均相等的正三棱柱ABC-A1B1C1中,
BB1=B1C1,且BB1⊥B1C1,
∴∠B1BC1=$\frac{π}{4}$.
∴异面直线AA1与BC1的夹角为$\frac{π}{4}$.
故选:B.
点评 本题考查异面直线所成角的求法,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,考查运用意识,是基础题.

练习册系列答案
相关题目
17.为便民惠民,某通信运营商推出“优惠卡活动”.其内容如下:卡号的前7位是固定的,后四位从“0000”到“9999”共10000个号码参与该活动,凡卡号后四位带有“6”或“8”的一律作为优惠卡,则“优惠卡”的个数是( )
| A. | 1980 | B. | 4096 | C. | 5904 | D. | 8020 |
19.$\frac{(x+y+1)^{5}}{xy}$展开式中的常数项为( )
| A. | 20 | B. | 10 | C. | 5 | D. | 1 |
16.已知复数z=cosθ+isinθ(i为虚数单位),则$z•\overline{z}$=( )
| A. | cos2θ | B. | 1 | C. | cos2θ | D. | cos2θ+isinθ |
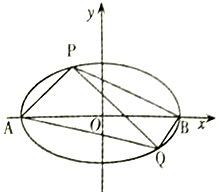 如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,A、B为椭圆的左右顶点,焦点到短轴端点的距离为2,P、Q为椭圆E上异于A、B的两点,且直线BQ的斜率等于直线AP斜率的2倍.
如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,A、B为椭圆的左右顶点,焦点到短轴端点的距离为2,P、Q为椭圆E上异于A、B的两点,且直线BQ的斜率等于直线AP斜率的2倍.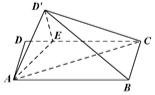 如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.
如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.