题目内容
19.$\frac{(x+y+1)^{5}}{xy}$展开式中的常数项为( )| A. | 20 | B. | 10 | C. | 5 | D. | 1 |
分析 变形(1+x+y)5=[1+(x+y)]5,按二项展开式求出xy项的系数,
即可得出$\frac{(x+y+1)^{5}}{xy}$展开式中的常数项.
解答 解:$\frac{(x+y+1)^{5}}{xy}$=$\frac{{[1+(x+y)]}^{5}}{xy}$
=${\;}_{\;}^{\;}$$\frac{{C}_{5}^{0}{+C}_{5}^{1}(x+y){{+C}_{5}^{2}(x+y)}^{2}+…}{xy}$
=$\frac{…{+C}_{5}^{2}•2xy+…}{xy}$
=…+2${C}_{5}^{2}$+…,
∴展开式中的常数项为2${C}_{5}^{2}$=20.
故选:A.
点评 本题考查了二项展开式的通项公式与应用问题,是基础题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
10.现行普通高中学生在高一升高二时面临着选文理科的问题,学校抽取了部分男、女学生意愿的一份样本,制作出如下两个等高堆积条形图:
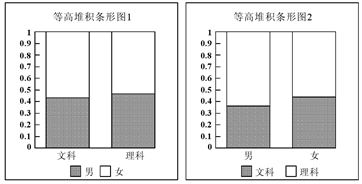
根据这两幅图中的信息,下列哪个统计结论是不正确的( )

根据这两幅图中的信息,下列哪个统计结论是不正确的( )
| A. | 样本中的女生数量多于男生数量 | |
| B. | 样本中有理科意愿的学生数量多于有文科意愿的学生数量 | |
| C. | 样本中的男生偏爱理科 | |
| D. | 样本中的女生偏爱文科 |
7.如图,在棱长均相等的正三棱柱ABC-A1B1C1中,异面直线AA1与BC1的夹角为( )
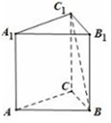

| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
14.经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:
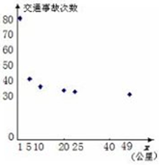
(Ⅰ)把界桩公里数1001记为x=1,公里数1005记为x=5,…,数据绘成的散点图如图所示,以x为解释变量、交通事故数y为预报变量,请在y=a+be-x和y=a+$\frac{b}{x}$间选取一个建立回归方程表述x,y二者之间的关系(a,b的值精确到0.1);
(Ⅱ)若保险公司在2015年交通事故中随机抽取100例,理赔60万元的有1例,理赔2万元的有19例,理赔0.2万元的有80例.
利用你得到的回归方程,试预报这一年在界桩1040公里附近处发生的交通事故的理赔费(理赔费精确到0.1万元).
附:回归直线v=$\widehat{α}$+$\widehat{β}$u的斜率和截距的最小二乘法估计分别为:
$\widehat{β}$=$\frac{\sum_{i=1}^{n}({u}_{i}-\overline{u})({v}_{i}-\overline{v})}{\sum_{i=1}^{n}({u}_{i}-\overline{u})^{2}}$,$\widehat{α}$=$\overline{v}$-$\widehat{β}$$\overline{u}$.
一些量的计算值:
表中:ωi=$\frac{1}{{x}_{i}}$,$\overline{ω}$=$\frac{1}{6}$$\sum_{i=1}^{6}{ω}_{i}$;φi=e${\;}^{-{x}_{i}}$,$\overline{φ}$=$\frac{1}{6}$$\sum_{i=1}^{6}{φ}_{i}$,$\frac{1}{40}$=0.025,e-40≈0.
| 界桩公里数 1001 | 1005 | 1010 | 1020 | 1025 | 1049 |
| 交通事故数 80 | 40 | 35 | 33 | 32 | 30 |

(Ⅰ)把界桩公里数1001记为x=1,公里数1005记为x=5,…,数据绘成的散点图如图所示,以x为解释变量、交通事故数y为预报变量,请在y=a+be-x和y=a+$\frac{b}{x}$间选取一个建立回归方程表述x,y二者之间的关系(a,b的值精确到0.1);
(Ⅱ)若保险公司在2015年交通事故中随机抽取100例,理赔60万元的有1例,理赔2万元的有19例,理赔0.2万元的有80例.
利用你得到的回归方程,试预报这一年在界桩1040公里附近处发生的交通事故的理赔费(理赔费精确到0.1万元).
附:回归直线v=$\widehat{α}$+$\widehat{β}$u的斜率和截距的最小二乘法估计分别为:
$\widehat{β}$=$\frac{\sum_{i=1}^{n}({u}_{i}-\overline{u})({v}_{i}-\overline{v})}{\sum_{i=1}^{n}({u}_{i}-\overline{u})^{2}}$,$\widehat{α}$=$\overline{v}$-$\widehat{β}$$\overline{u}$.
一些量的计算值:
| $\overline{x}$ | $\overline{y}$ $\overline{ω}$ $\overline{φ}$ | $\sum_{i=1}^{6}({ω}_{i}-\overline{ω})^{2}$ | $\sum_{i=1}^{6}({φ}_{i}-\overline{φ})^{2}$ | $\sum_{i=1}^{6}({ω}_{i}-\overline{ω})({y}_{i}-\overline{y})$ | $\sum_{i=1}^{6}({φ}_{i}-\overline{φ})({y}_{i}-\overline{y})$ |
| 18.3 | 41.7 0.235 0.062 | 0.723 | 0.112 | 36.3 | 14.1 |
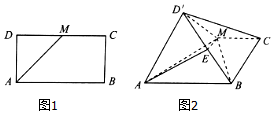 如图,矩形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.
如图,矩形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.