题目内容
16．已知复数z=cosθ+isinθ（i为虚数单位），则$z•\overline{z}$=（ ）| A． | cos2θ | B． | 1 | C． | cos2θ | D． | cos2θ+isinθ |
分析 利用复数的乘法运算性质即可得出．
解答 解：复数z=cosθ+isinθ（i为虚数单位），
则$z•\overline{z}$=（cosθ+isinθ）（cosθ-isinθ）=cos2θ+sin2θ=1．
故选：B．
点评 本题考查了复数的乘法运算性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
春雨教育同步作文系列答案
相关题目
6．已知函数f（x）=$\sqrt{3}$sin（2x-φ）-cos（2x-φ）（|φ|＜$\frac{π}{2}$）的图象关于y轴对称，则f（x）在区间$[{-\frac{π}{6}，\frac{π}{3}}]$上的最大值为（ ）
| A． | 1 | B． | $\sqrt{3}$ | C． | $\sqrt{2}$ | D． | 2 |
7．如图，在棱长均相等的正三棱柱ABC-A1B1C1中，异面直线AA1与BC1的夹角为（ ）
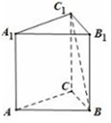
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
1．已知f（x）=$\frac{e^x}{{{x^2}+a}}（{a＞0}）$的两个极值点分别为x1，x2（x1＜x2），则a（lnx1+lnx2）的取值范围是（ ）
| A． | $[{-\frac{1}{e}，0}）$ | B． | （0，+∞） | C． | （0，1） | D． | $[{-\frac{1}{e}，+∞}）$ |
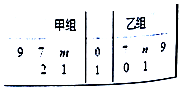某车间将10名技工平均分成甲、乙两组加工某种零件，在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示．已知两组技工在单位时间内加工的合格零件平均数都为9．