题目内容
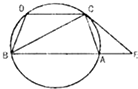如图，已知圆上的弧 |
| AC |
|
| BD |
（1）∠ACE=∠BCD；
（2）
| BC2 |
| EC2 |
| CD |
| EA |
考点：与圆有关的比例线段
专题：选作题,立体几何
分析：（1）先根据题中条件：“
=
，”，得∠BCD=∠ABC．再根据EC是圆的切线，得到∠ACE=∠ABC，从而即可得出结论．
（II）证明△BDC～△ECB，可得BC2=BE×CD．由切割线定理可得EC2=EA×EB，两式相除可得结论．
|
| AC |
|
| BD |
（II）证明△BDC～△ECB，可得BC2=BE×CD．由切割线定理可得EC2=EA×EB，两式相除可得结论．
解答：
解：（1）因为
=
，所以∠BCD=∠ABC．
又因为EC与圆相切于点C，
故∠ACE=∠ABC
所以∠ACE=∠BCD．（5分）
（2）因为∠ECB=∠CDB，∠EBC=∠BCD，
所以△BDC～△ECB，
故
=
．
即BC2=BE×CD．
由切割线定理可得EC2=EA×EB，
两式相除可得
=
．（10分）
|
| AC |
|
| BD |
又因为EC与圆相切于点C，
故∠ACE=∠ABC
所以∠ACE=∠BCD．（5分）
（2）因为∠ECB=∠CDB，∠EBC=∠BCD，
所以△BDC～△ECB，
故
| BC |
| BE |
| CD |
| BC |
即BC2=BE×CD．
由切割线定理可得EC2=EA×EB，
两式相除可得
| BC2 |
| EC2 |
| CD |
| EA |
点评：本题主要考查圆的切线的判定定理的证明、弦切角的应用、三角形相似等基础知识，考查运化归与转化思想．属于基础题．
练习册系列答案
巧学巧练系列答案
相关题目