Question

9．已知函数y=f（x）是定义在R上的偶函数，且f（x+1）=f（x-1），当x∈[0，1]时，f（x）=2^x-1，则函数g（x）=f（x）-ln$\frac{x}{2}$的零点个数为4．

Answer 1

分析 函数g（x）=f（x）-ln$\frac{x}{2}$的零点个数可化为f（x）与y=ln$\frac{x}{2}$的图象的交点的个数，从而作出函数f（x）与y=ln$\frac{x}{2}$的图象求解即可．

解答 解：函数g（x）=f（x）-ln$\frac{x}{2}$的零点个数可化为f（x）与y=ln$\frac{x}{2}$的图象的交点的个数，
作函数f（x）与y=ln$\frac{x}{2}$的图象如下，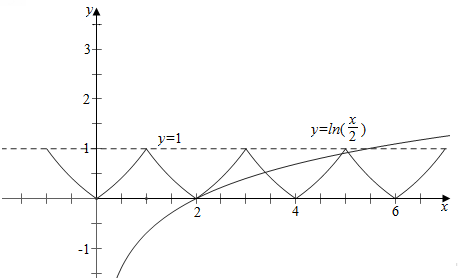

结合图象可知，
函数f（x）与y=ln$\frac{x}{2}$的图象有四个交点，
故函数g（x）=f（x）-ln$\frac{x}{2}$的零点个数为4，
故答案为：4．

点评 本题考查了学生的作图能力及数形结合的思想应用，同时考查了函数的性质的判断与应用．