题目内容
19.以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,若椭圆C两焦点的极坐标分别是$(\sqrt{2},0),(\sqrt{2},π)$,长轴长是4.(I)求椭圆C的参数方程;
(Ⅱ)在直角坐标系xOy中,曲线C的参数方程为$\left\{\begin{array}{l}{x=cosα}\\{y=1+sinα}\end{array}\right.$(α为参数),以O为极点,x轴的正半轴为极轴建立极坐标系,求曲线C的极坐标方程.
分析 (Ⅰ)先求出椭圆C两焦点的直角坐标,由此能求出椭圆直角坐标方程,从而能求出椭圆C的参数方程.
(Ⅱ)先求出曲线C的普通方程,由此能求出曲线C的极坐标方程.
解答 解:(Ⅰ)∵椭圆C两焦点的极坐标分别是$(\sqrt{2},0),(\sqrt{2},π)$,
∴椭圆C两焦点的直角坐标分别是($\sqrt{2}$,0),(-$\sqrt{2}$,0),
∵长轴长是4,∴a=2,c=$\sqrt{2}$,b=$\sqrt{4-2}$=$\sqrt{2}$,
∴椭圆方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$.
∴椭圆C的参数方程:$\left\{\begin{array}{l}{x=2cosθ}\\{y=\sqrt{2}sinθ}\end{array}\right.$,0≤θ<π.
(Ⅱ)∵曲线C的参数方程为$\left\{\begin{array}{l}{x=cosα}\\{y=1+sinα}\end{array}\right.$(α为参数),
∴曲线C的普通方程为x2+(y-1)2=1,即x2+y2-2y=0,
∴曲线C的极坐标方程为ρ2-2ρsinθ,即ρ=2sinθ.
点评 本题考查椭圆的参数方程和曲线的极坐标方程的求法,是基础题,解题时要认真审题,注意极坐标方程、直角坐标方程、参数方程、普通方程互化公式的合理运用.

练习册系列答案
相关题目
14.若集合M={x|1<x<4},N={x|x2-7x<0},则M∩N等于( )
| A. | {x|0<x<4} | B. | {x|1<x<7} | C. | {x|1<x<4} | D. | {x|4<x<7} |
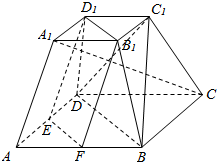 如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,E、F分别是AD、AB的中点.求证:平面EFB1D1∥平面BDC1.
如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,E、F分别是AD、AB的中点.求证:平面EFB1D1∥平面BDC1.