题目内容
设函数f(x)=
,则函数g(x)=f(x)+
的零点个数为 个.
|
| 1 |
| 2 |
考点:函数零点的判定定理
专题:作图题,函数的性质及应用
分析:问题等价于函数y=f(x)与函数y=-
图象的公共点个数,作出函数的图象可得.
| 1 |
| 2 |
解答:
 解:函数g(x)=f(x)+
解:函数g(x)=f(x)+
的零点个数等价于函数y=f(x)与函数y=-
图象的公共点个数,
作出它们的图象可得公共点个数为3,
故答案为:3
 解:函数g(x)=f(x)+
解:函数g(x)=f(x)+| 1 |
| 2 |
| 1 |
| 2 |
作出它们的图象可得公共点个数为3,
故答案为:3
点评:本题考查函数零点的个数问题,转化为函数图象的公共点个数是解决问题的关键,属基础题.

练习册系列答案
相关题目
已知O是锐角△ABC的外心,若
=x
+y
(x,y∈R),则( )
| OC |
| OA |
| OB |
| A、x+y≤-2 |
| B、-2≤x+y<-1 |
| C、x+y<-1 |
| D、-1<x+y<0 |
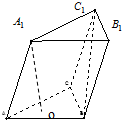 已知三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面△ABC的中心,如图所示:
已知三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面△ABC的中心,如图所示: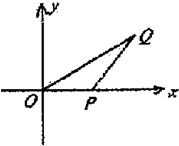 如图已知△OPQ的面积为S,且
如图已知△OPQ的面积为S,且