题目内容
当x,y满足不等式组
时,点(4,0)为目标函数z=ax-2y取得最大值时的唯一最优解,则实数a的取值范围是( )
|
| A、(-∞,-2] |
| B、(-∞,-2) |
| C、[-2,+∞) |
| D、(-2,+∞) |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用目标函数的几何意义,利用目点(4,0)为目标函数z=ax-2y取得最大值时的唯一最优解,讨论目标函数的斜率满足的条件,从而求出a的取值范围.
解答:
解:作出不等式组对应的平面区域如图:(阴影部分ABC).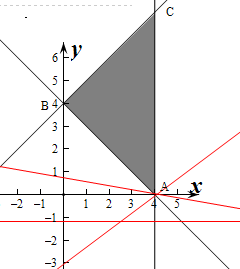
则A(4,0)由z=ax-2y得y=
ax-
z,即直线的截距最大,z最小.
平移直线y=
ax-
z,则直线的截距最大,z最小.
要使点(4,0)为目标函数z=ax-2y取得最大值时的唯一最优解,
则满足:
①当a<0时,y=
ax-
z此时目标函数的斜率
a≥-1,即-2≤a<0,
②当a=0时,满足条件,
③当a>0时,满足条件,
综上a≥-2
故选:C

则A(4,0)由z=ax-2y得y=
| 1 |
| 2 |
| 1 |
| 2 |
平移直线y=
| 1 |
| 2 |
| 1 |
| 2 |
要使点(4,0)为目标函数z=ax-2y取得最大值时的唯一最优解,
则满足:
①当a<0时,y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②当a=0时,满足条件,
③当a>0时,满足条件,
综上a≥-2
故选:C
点评:本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
已知y=f(x)是偶函数,且在区间(0,+∞)上是增函数,则f(-4)、f(π)、f(-1)的大小关系是( )
| A、f(π)>f(-1)>f(-4) |
| B、f(-1)>f(-4)>f(π) |
| C、f(-4)>f(π)>f(-1) |
| D、f(-4)>f(-1)>f(π) |
函数y=log2(1-x)的定义域是( )
| A、[1,+∞) |
| B、(-∞,1] |
| C、(1,+∞) |
| D、(-∞,1) |
已知i是虚数单位,若z(3-4i)=4+3i,则|z|=( )
| A、1 | ||
B、
| ||
| C、5 | ||
| D、10 |
已知sin(a+
)=-
,-
<a<0,则cos(a+
)等于( )
| π |
| 3 |
| 5 |
| 13 |
| π |
| 2 |
| 2π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知a∈R,则“a2>2a”是“a>2”成立的( )
| A、充分不必要 |
| B、必要不充分 |
| C、充分必要 |
| D、既不充分也不必要 |
已知{an}为等差数列,若a2=3,a4=5,则a1的值为( )
| A、1 | B、2 | C、3 | D、4 |
设a=2cos228°-1,b=
(cos18°-sin18°),c=log
,则( )
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| A、a<b<c |
| B、b<a<c |
| C、b<c<a |
| D、c<b<a |