题目内容
17.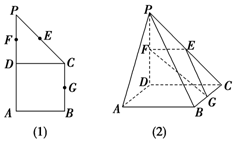 如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).
如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).(1)求证:AP∥平面EFG;
(2)若点Q是线段PB的中点,求证:PC⊥平面ADQ.
分析 (1)由条件可得EF∥CD∥AB,利用直线和平面平行的判定定理证得EF∥平面PAB.同理可证,EG∥平面PAB,可得平面EFG∥平面PAB.再利用两个平面平行的性质可得AP∥平面EFG.
(2)由条件可得DA、DP、DC互相垂直,故AD⊥平面PCD,AD⊥PC.再由EQ平行且等于$\frac{1}{2}$BC可得EQ平行且等于$\frac{1}{2}$AD,故ADEQ为梯形.再根据DE为等腰直角三角形PCD 斜边上的中线,可得DE⊥PC.再利用直线和平面垂直的判定定理证得PC⊥平面ADQ.
解答  解:(1)证明:E、F、G分别为线段PC、PD、BC的中点,
解:(1)证明:E、F、G分别为线段PC、PD、BC的中点,
可得EF∥CD∥AB.
由于AB?平面PAB,EF不在平面 PAB内,故有 EF∥平面PAB.
同理可证,EG∥平面PAB.
由于EF、EG是平面EFG内的两条相交直线,
故有平面EFG∥平面PAB.
而PA?平面PAB,∴AP∥平面EFG.
(2)由条件可得,CD⊥AD,CD⊥PD,
而PD、AD是两条相交直线,故CD⊥平面PAD,
∴∠PDA 为二面角PCD-CD-ABCD的平面角.
再由平面PCD⊥平面ABCD,可得PD⊥AD,故DA、DP、DC互相垂直,故AD⊥平面PCD,
而PC?平面PCD,故有AD⊥PC.
∵点Q是线段PB的中点,∴EQ平行且等于$\frac{1}{2}$BC,∴EQ平行且等于$\frac{1}{2}$AD,故四边形ADEQ为梯形.
再由AD=DC=PD=2,可得DE为等腰直角三角形PCD 斜边上的中线,∴DE⊥PC.
这样,PC垂直于平面ADQ中的两条相交直线AD、DE,∴PC⊥平面ADQ.
点评 本题主要考查直线和平面平行的判定定理、直线和平面垂直的判定定理的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.若直线L1:x+ay+6=0与直线L2:(a-2)x+3y+2a=0互相平行,则a的值为( )
| A. | -1或3 | B. | 1或3 | C. | -1 | D. | 以上都不对 |
8.设直线l经过椭圆$\frac{x^2}{4}+{y^2}=1$的右焦点且倾斜角为45°,若直线l与椭圆相交于A,B两点,则|AB|=( )
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{8}{5}$ |
2.一条直线与两条异面直线中的一条平行,则它和另一条的位置关系是( )
| A. | 异面 | B. | 相交 | C. | 异面或平行 | D. | 相交或异面 |
7.近年来我国电子商务行业发展迅速,相关管理部门推出了针对电商的商品质量和服务评价的评价体系,现从评价系统中选出某商家的200次成功交易,发现对商品质量的好评率为0.6,对服务评价的好评率为0.75,其中对商品质量和服务评价都做出好评的交易80次.
(1)是否可以在犯错误概率不超过0.5%的前提下,认为商品质量与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的5次购物中,设对商品质量和服务评价全好评的次数为随机变量X,求X的分布列(可用组合数公式表示)和数学期望.
参考公式:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
(1)是否可以在犯错误概率不超过0.5%的前提下,认为商品质量与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的5次购物中,设对商品质量和服务评价全好评的次数为随机变量X,求X的分布列(可用组合数公式表示)和数学期望.
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
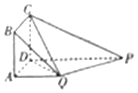 如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,2QA=2AB=PD
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,2QA=2AB=PD