题目内容
18.已知函数f(x)=ax2-bx+lnx,(a,b∈R).(1)若a=1,b=3,求函数f(x)的单调递增区间;
(2)若b=0时,不等式f(x)≤0在[1,+∞)上恒成立,求实数a的取值范围;
(3)当a=1,b>$\frac{9}{2}$时,记函数f(x)的导函数f'(x)的两个零点是x1,x2(x1<x2),求证:f(x1)-f(x2)>$\frac{63}{16}$-3ln2.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)问题转化为a≤-$\frac{lnx}{{x}^{2}}$在区间[1,+∞)恒成立,令h(x)=-$\frac{lnx}{{x}^{2}}$,根据函数的单调性求出a的范围即可;
(3)由题意得x1,x2(x1<x2)是方程2x2-bx+1=0的两个根,记g(x)=2x2-bx+1,根据函数的单调性证明即可.
解答 解:(1)由题意得:x>0,a=1,b=3时,f(x)=x2-3x+lnx,
f′(x)=2x-3+$\frac{1}{x}$=$\frac{(2x-1)(x-1)}{x}$,
令f′(x)>0,解得:0<x<$\frac{1}{2}$或x>1,
故f(x)在(0,$\frac{1}{2}$),(1,+∞)递增;
(2)b=0时,f(x)=ax2+lnx,
不等式f(x)≤0在[1,+∞)恒成立,
即a≤-$\frac{lnx}{{x}^{2}}$在区间[1,+∞)恒成立,
令h(x)=-$\frac{lnx}{{x}^{2}}$,则h′(x)=-$\frac{2lnx-1}{{x}^{3}}$,
令h′(x)>0,解得:x>$\sqrt{e}$,
令h′(x)<0,解得:1<x<$\sqrt{e}$,
故f(x)在(1,$\sqrt{e}$)递减,在($\sqrt{e}$,+∞)递增,
故h(x)min=h($\sqrt{e}$)=-$\frac{1}{2e}$,
故a≤-$\frac{1}{2e}$;
(3)证明:a=1时,f(x)=x2-bx+lnx,f′(x)=$\frac{{2x}^{2}-bx+1}{x}$,(x>0),
由题意得x1,x2(x1<x2)是方程2x2-bx+1=0的两个根,
记g(x)=2x2-bx+1,则g($\frac{1}{b}$)=$\frac{2}{{b}^{2}}$>0,
∵b>$\frac{9}{2}$,∴g($\frac{1}{4}$)=$\frac{1}{4}$($\frac{9}{2}$-b)<0,g(2)=9-2b<0,
∴x1∈($\frac{1}{b}$,$\frac{1}{4}$),x2∈(2,+∞),且f(x)在[x1,x2]递减,
故f(x1)-f(x2)>f($\frac{1}{4}$)-f(2)=$\frac{7b}{4}$-$\frac{63}{16}$-3ln2,
∵b>$\frac{9}{2}$,∴f(x1)-f(x2)>$\frac{7}{4}$•$\frac{9}{2}$-$\frac{63}{16}$-3ln2=$\frac{63}{16}$-3ln2.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,考查转化思想,是一道综合题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | p假q假 | B. | p假q真 | C. | p真q假 | D. | p真q真 |
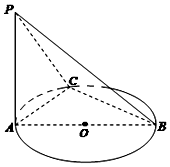 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则二面角A-BC-P的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则二面角A-BC-P的大小为( )