题目内容
17.在△ABC中,内角A,B,C的对边分别为a,b,c,若cosA=$\frac{7}{8}$,c-a=2,b=3,则a等于( )| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
分析 由已知条件和余弦定理可得a的方程,解方程可得.
解答 解:由题意可得c=a+2,b=3,cosA=$\frac{7}{8}$,
∴由余弦定理可得cosA=$\frac{1}{2}$•$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{bc}$,
代入数据可得$\frac{7}{8}$=$\frac{9+(a+2)^{2}-{a}^{2}}{2×3(a+2)}$,
解方程可得a=2
故选:A
点评 本题考查余弦定理,属基础题.

练习册系列答案
相关题目
8.方程3x+4x=5x解的情况是( )
| A. | 有且只有一个根2 | B. | 不仅有根2还有其他根 | ||
| C. | 有根2和另一个负根 | D. | 有根2和另一个正根 |
2.已知等边△ABC的边长为2,若$\overrightarrow{BC}$=3$\overrightarrow{BE}$,$\overrightarrow{AD}$=$\overrightarrow{DC}$,则$\overrightarrow{BD}$•$\overrightarrow{AE}$等于( )
| A. | -2 | B. | -$\frac{10}{3}$ | C. | 2 | D. | $\frac{10}{3}$ |
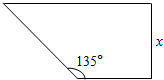 某植物园要建形状为直角梯形的苗圃(如图所示),两条邻边借用夹角为135°的两面墙,另两条边的总长为60m,设垂直于底边的腰长为x(m).
某植物园要建形状为直角梯形的苗圃(如图所示),两条邻边借用夹角为135°的两面墙,另两条边的总长为60m,设垂直于底边的腰长为x(m).